Scikit-learn笔记4(ROC曲线)

源文件

Applied Machine Learning in Python

这门课实在是太差了. 严重差评:

"所谓私人恩怨，跟政治就是一回事。所以，如果有哪个白痴政客或者哪个大人物想要推行一项法令或政策，伤害到你或者你亲人朋友的利益，那就是私人恩怨。点燃你的怒火吧。" ----奎尔

作为报复, 我决定把第三周的ppt给丫翻译了!

决策函数(decision_function)

  • 分类器对每个测试点都给出一个分数, 这个分数表示分类器预测的可信度.
  • 选择一个固定的决策阈值就给出了一个分类规则. (大于阈值的就是正分类, 小于阈值的就是负分类)
  • 通过改变决策阈值, 在所有可能的分数范围内扫描, 我们就可以给出给出一个曲线

预测属于某个分类的概率(predict_proba)

典型的规则: 选择最可能的分类 例如: 如果数值>0.5, 属于分类1

  • 通过改变阈值可以调节分类器的预测.
  • 更高的阈值导致更为保守的分类器
    • 例如只有数值>0.7才归入分类1
    • 高阈值增加了precision. 比之前低阈值时更少把样本归入分类1, 但是如果归入到样本1, 那么把握更大.

还是举个我更熟悉的例子吧, 比如仅仅用眼压作为青光眼的诊断标准,

  • 21mmHg就是一个阈值,
  • 大于21mmHg的就归入青光眼分类, 小于等于21mmHg的就归入正常眼的分类. 但显然这样会把一部分高眼压症的人算作是青光眼.
  • 如果把阈值提高到比如30mmHg, 那么筛出来的病人, 真正就是青光眼的可能性就要高很多. 就是Precision更高.
  • 如果把阈值降低到比如15mmHg, 那么就有更少的病人漏网, 也就是Recall更高
  • 后面会讲半天ROC曲线, 就是看阈值变化时, Precision和Recall的变化.

但是! 在此处吐槽一下. 这样的分类方法明显是错的啊, 本来根本不是用一个值来简单区分的事情, 为什么要强行这么做? 要诊断青光眼还要看视盘, 看盘沿, 看视野, 看动态变化, 本来就不是一个一维的事情, 不管其他, 去找一个参数的分界线是不对的啊.

_贱人就是矫情_

(4月4日更正), 此处的吐槽是不对的, 很抱歉. decision_function可以用到不同的分类器上, 是把多维的数据最终映射到一维上, 再拿到一维上来分类, 所以即使是深度学习, 如果是二分类问题, 仍然是最后由一个神经元输出[0, 1]之间的值, 并根据这个值来区分, 比如用sigmoid做激活函数, 那么分界阈值就是0.5, 但实际上可以设定不同. 所以仍然可以得出一个ROC曲线.

复习一下各种率

Accuracy

  • 正确率
  • 有病没病都说对了的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ Accuracy=\frac{100+110+120}{100+6+11+1+110+12+2+7+120} $$

Recall

  • 敏感性, 检出率, 真阳性率.
  • 实际有病, 测出有病的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ Recall=\frac{120}{2+7+120} $$

Precision

  • 精确度, 阳性预测率, PPV
  • 测出有病, 还说对了的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ Precision=\frac{120}{11+12+120} $$

Specificity

  • 特异性, 真阴性率
  • 测出没病, 还说对了的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ Specificity=\frac{100+6+1+110}{100+6+1+110+2+7} $$

False Positive Rate

  • 假阳性率, 误报率
  • 本来没病, 测出有病的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ False Positive Rate=\frac{11+12}{100+6+11+1+110+12} $$

比如现在只用眼压区分青光眼, 补充一点背景知识: 已知95%的人群眼压是是10-21mmHg, 眼压最低也只能到房水的流出通道, 也就是静脉里面, 最低最低8mmHg, 眼压到30mmHg摸起来已经接近脑门的硬度了, 到40mmHg已经要疼得撞墙了.

  • 那么, 如果以10mmHg作为分界, 认为大于10mmHg的都是青光眼, 那么几乎所有的人类都是青光眼, 于是没有任何一个青光眼病人会被漏掉.
  • 如果以40mmHg作为分界, 认为大于40mmHg的才是青光眼, 那么只有急性发作的病人才会被当作是青光眼, 这时候每筛出一个病人, 肯定就是青光眼, 不会筛出来的不是, 但会漏掉很多病人.

Precision-Recall曲线

  • X轴: Precision
  • Y轴: Recall

右上顶端:

  • 理想点
  • Precision=1.0
  • Recall=1.0

P-R曲线的陡峭程度很重要. 在最大Precision时, 能够达到多大的Recall.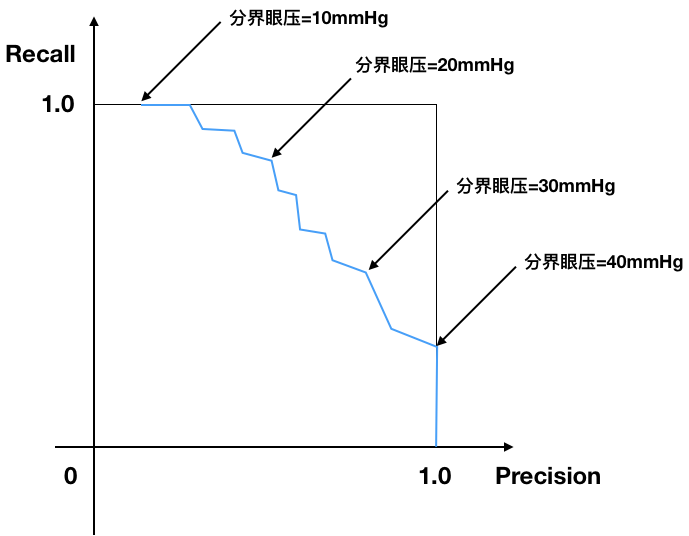
P-R_curve.png

ROC曲线

  • X轴: False Positive Rate 假阳性率
  • Y轴: True Positive Rate 真阳性率

左上顶点:

  • 理想点
  • False positive rate 假阳性率=0
  • True positive rate 真阳性率=1

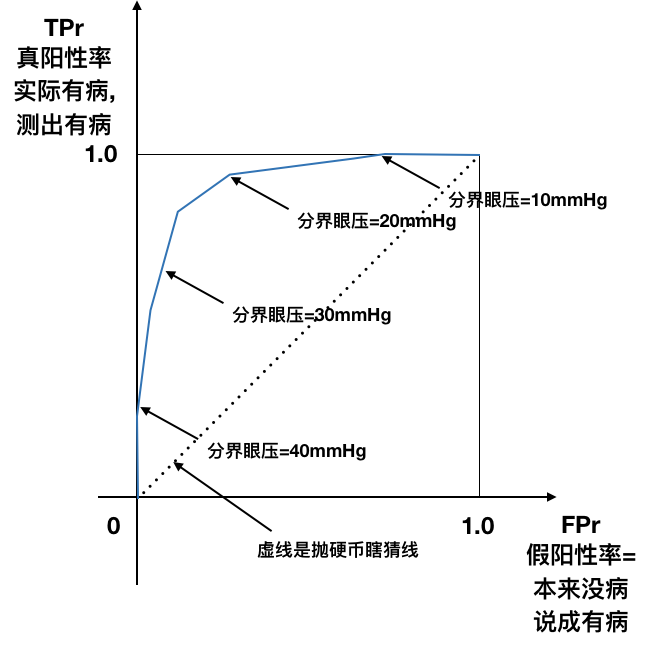
ROC.png

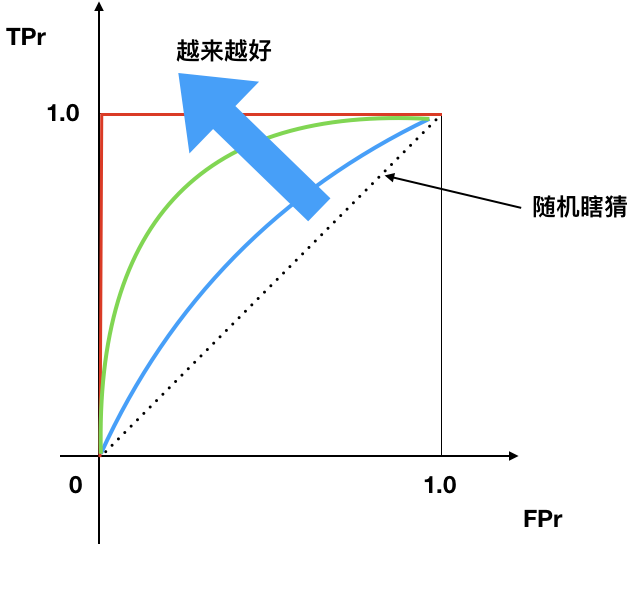
  • ROC曲线越往左上, 越好.
  • 曲线下面积(AUC), 越大越好
  • 45度线是随机瞎猜线

ROC-2.png

未完待续

In [ ]: