极简metalens(1)

源文件

这篇极简科普是关于:

  • metalens
  • metasurface, 超表面, 超颖表面
  • Pancharatnam Berry Phase
  • 几何相位, 贝里相位

这些都是一个领域的东西.

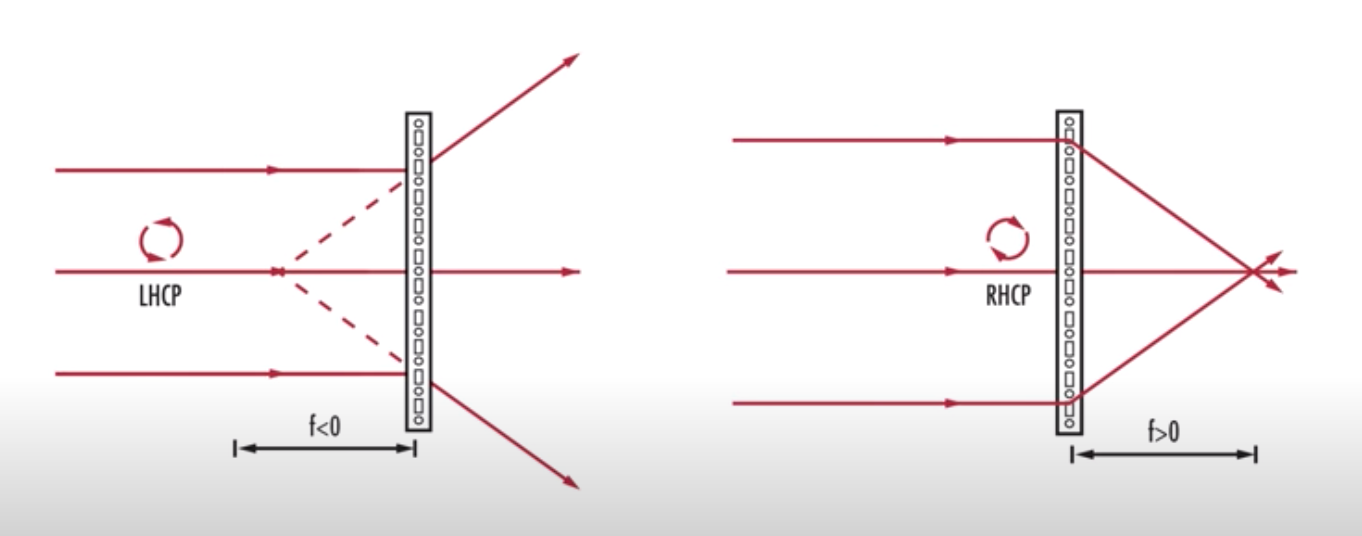
近期研读VR文献和专利, 反复发现Pancharatnam Berry Phase透镜这个东西, 如果入射光是圆偏振光, 可以产生相反的屈光度, 比如对于右旋圆偏振光(RCP)是+3D的透镜, 对于左旋圆偏振光(LCP)的就是-3D, 实在是非常魔法.

作为一个已经认真学习本领域技术1整天, 认识本领域专家的学生的师兄的哥们的, 不写剧情与人物的科幻小说(发明专利)作家. 我认为自己已经有足够的资格来撰写一篇极简科普. (没错我就是在黑各种极简).

本极简科普是以临床眼科医生为假设读者撰写的, 就是那些听见“像差”就呵呵, 看见公式就晕过去的家伙们.

波前 wavefront

光是电磁波, 一束光把相同的相位连起来, 就形成了波前(wavefront)

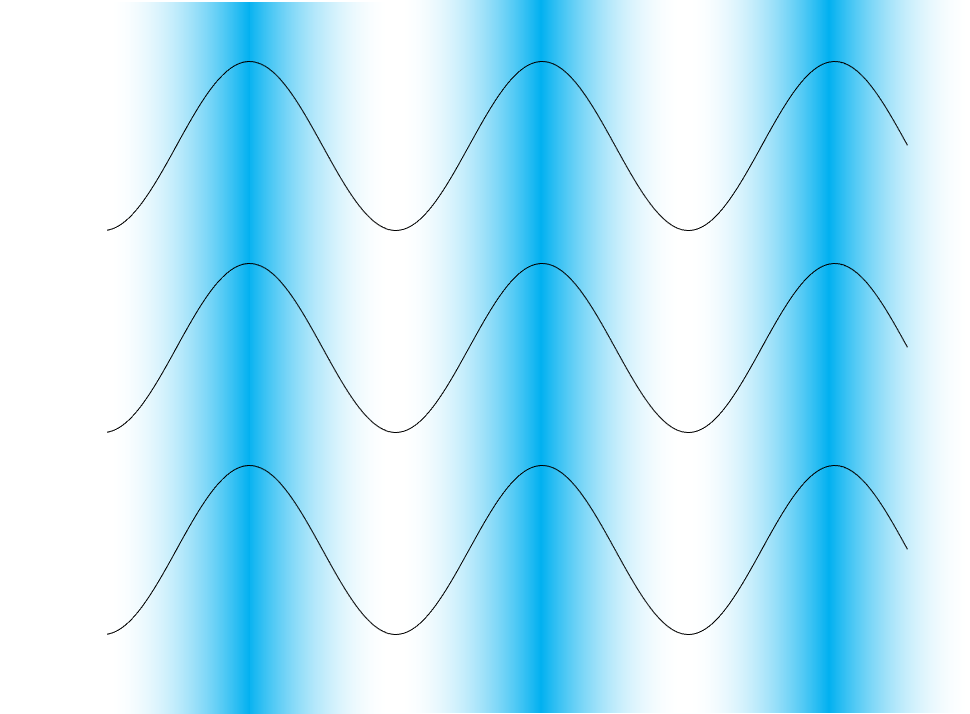
wavefront

平行光就是平面波传播, 汇聚光就是球面波.

折射

温故而知新, 先推导一遍折射定律Snell定律.

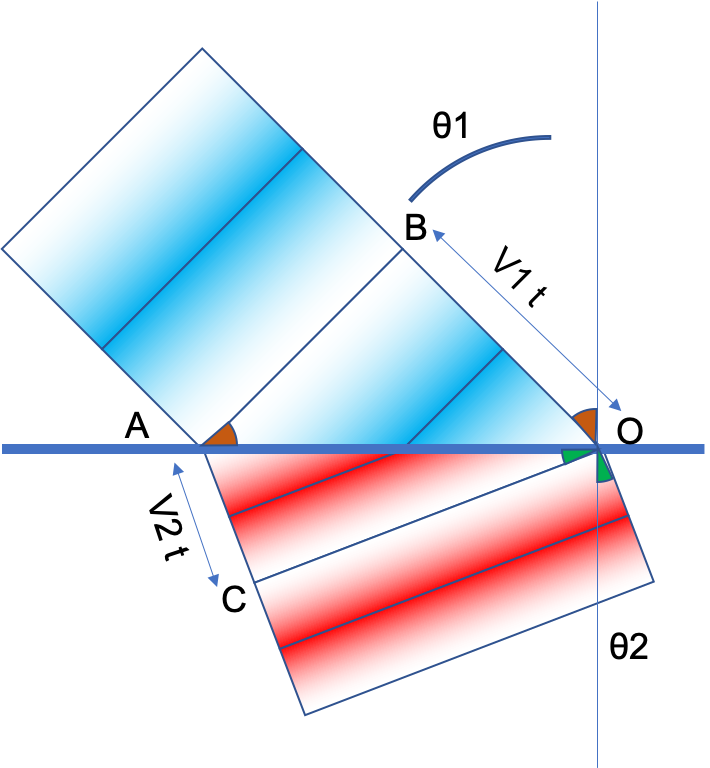
一束平行光以θ1的入射角入射到界面上, 以θ2的角度出射. snell

A点接触到界面时, 同相位的B点还没到, 如果在介质1里的速度是V1=C/n1, 经过t时间B才走到界面上的点O, 那么:

当B到达O点的时候, A点的波已经继续走了, 按照介质2中的速度V2=C/n2, 走到了C点, 那么:

两个式子中的t是一样的, AO是一样的, 所以整理一下:

再把V1=C/n1, V2=C/n2代入, 得到:

这就是中学就学过的折射定律, 又叫Snell定律.

注意在界面折射时, 我用的颜色深浅两侧是一样的. 也就是说在界面上, 相位是不变的, 两侧是连续的.

连续的波

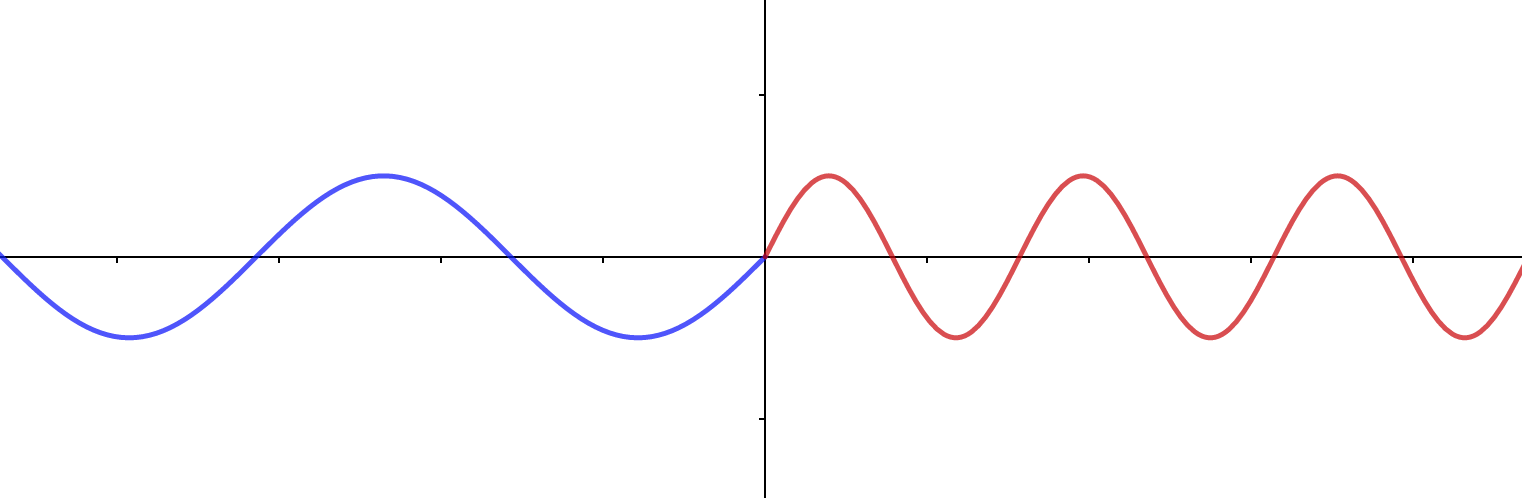
扩展Snell定律

但是如果在折射界面上有相位的突变:

相位突变

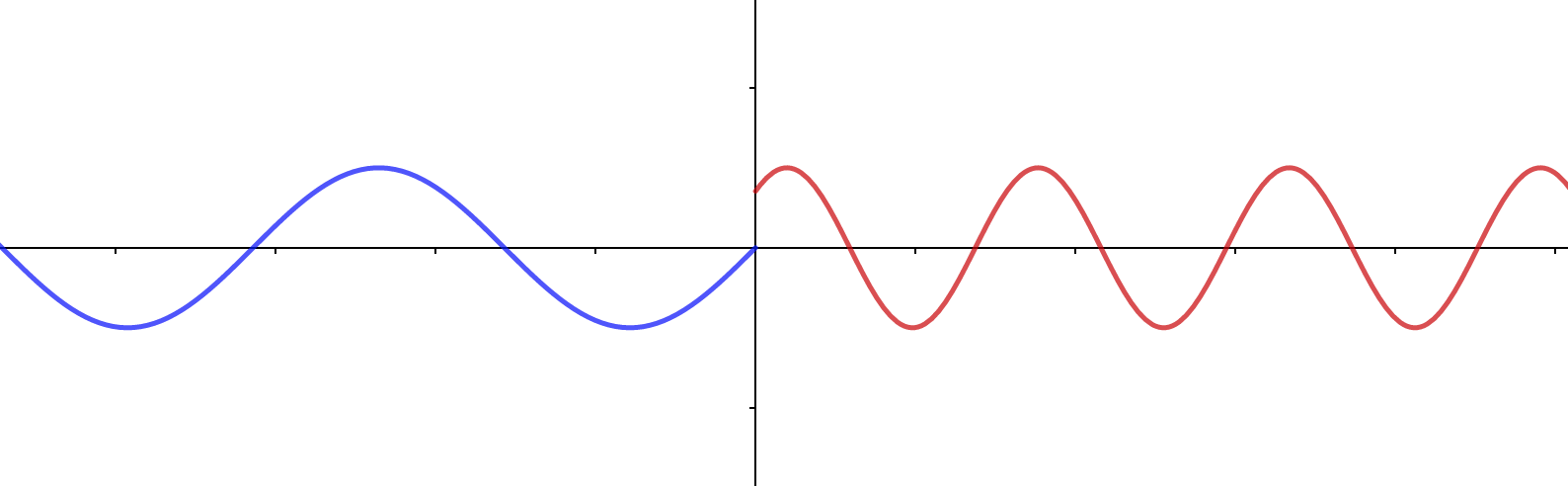
而且如果相位突变的程度还和位置有关:

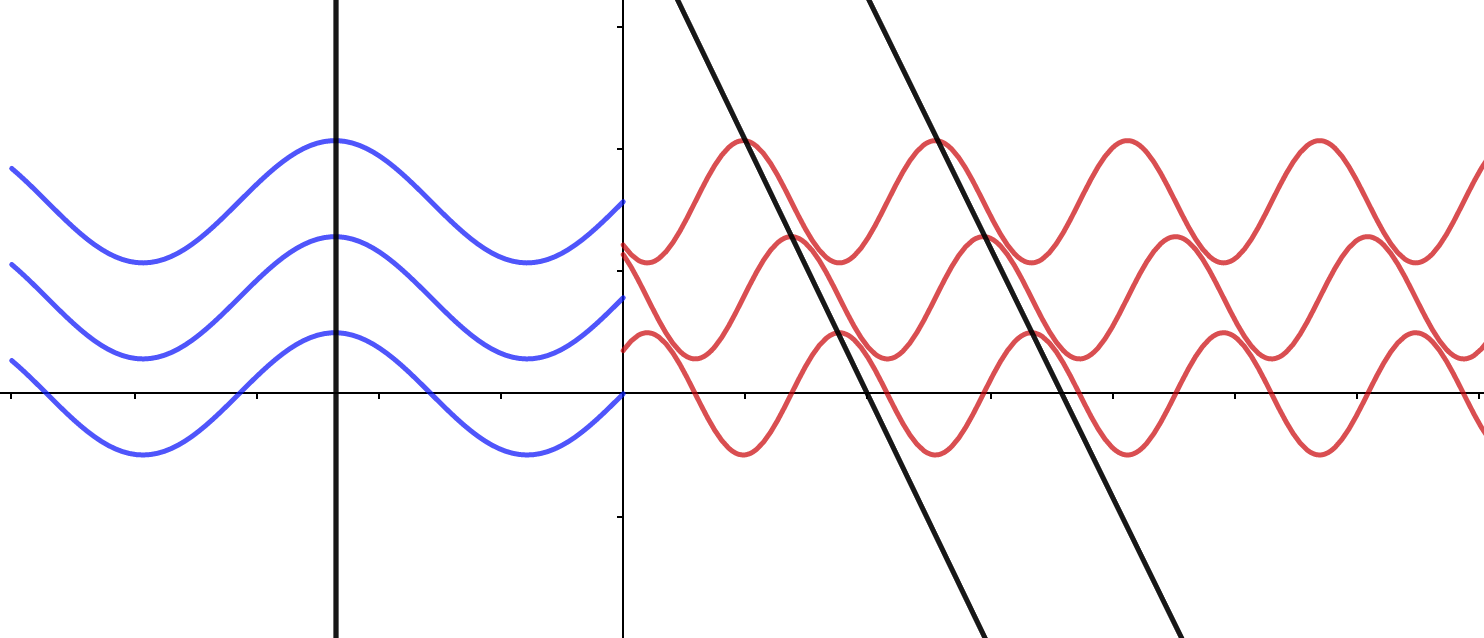
相位突变2

那么相位突变本身就可能使光线转向. 于是可能会出现诡异的折射过程:

图片 1

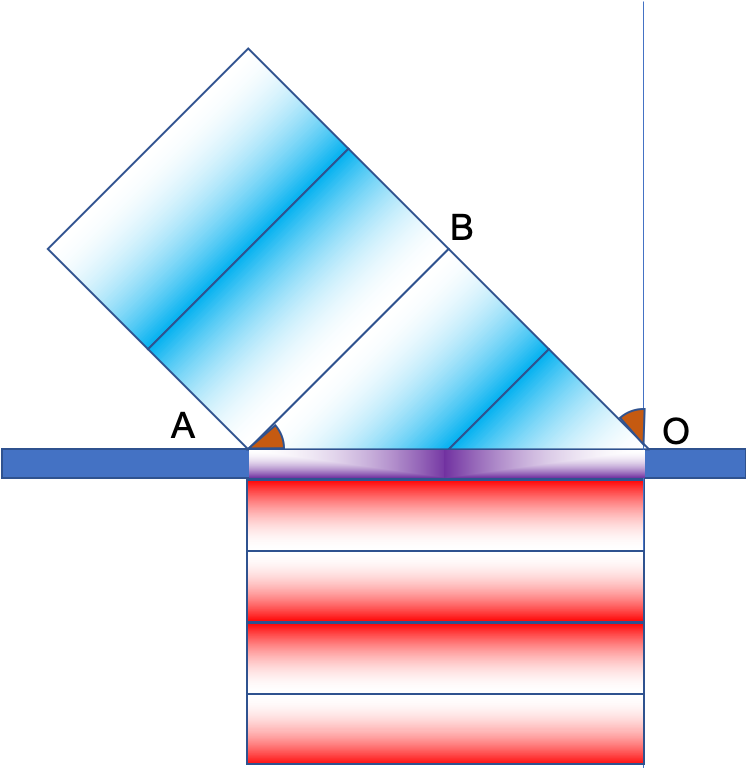
如果在AO界面上, 有一个能够改变相位东西, 不同位置x, 对应的改变量是Φ(x), 那么snell定律就重新写成了:

总之如果你能够在界面上把相位随意调整0~2π, 那就可以随心所欲控制光的传播方向了.

用天线改变相位

光是电磁场, 所以可以用控制电磁场的方法来控制. 比如用天线把电磁波收下来, 然后变个相位再发射出去. 对于光来说, 就是一块小于波长的导线. (太佩服了)

最简单的就是金属圆柱立在玻璃上. 圆柱高度恒定时, 直径不同就能够产生不同的相位差. 尺寸和波长有关的.

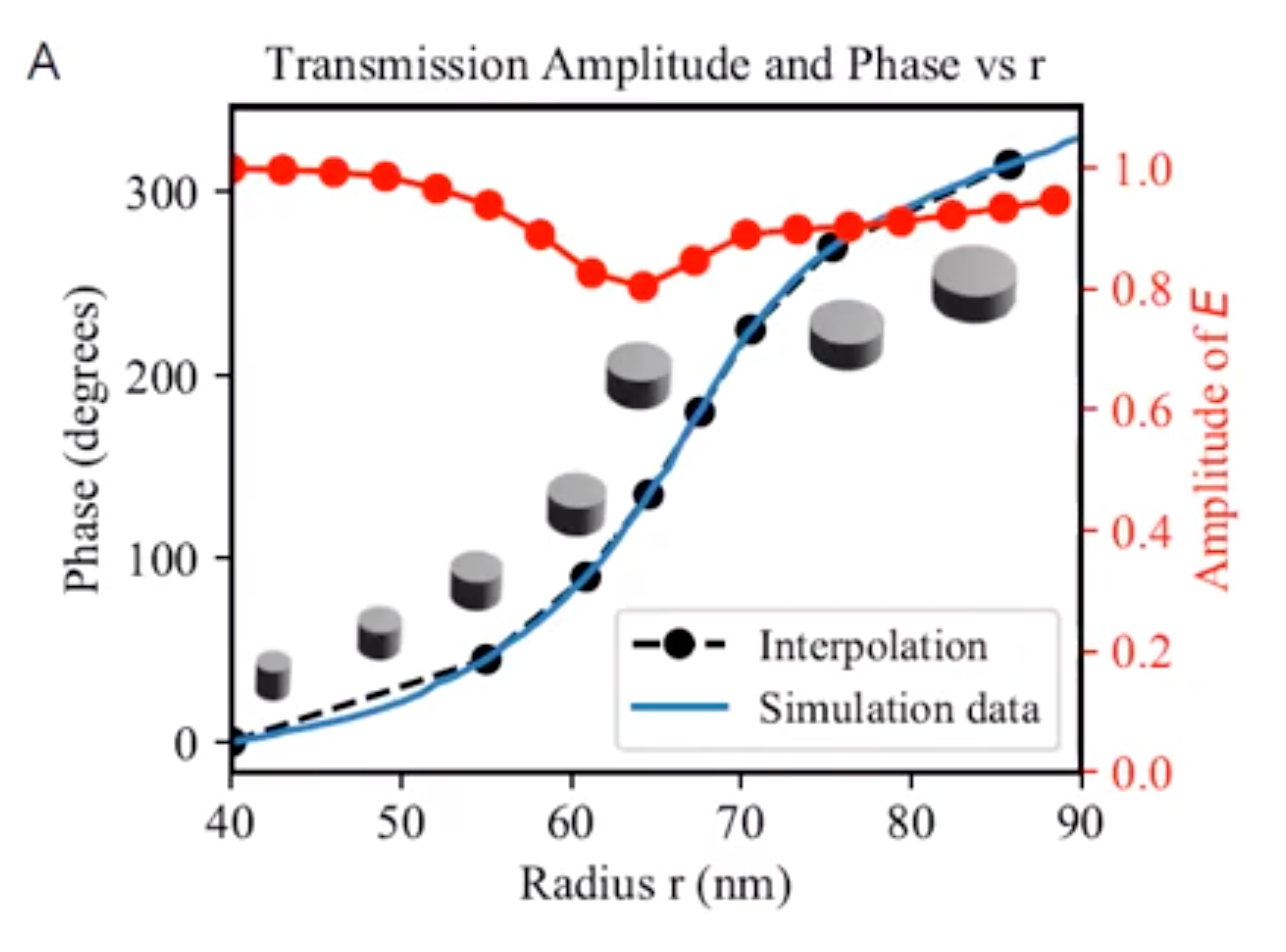
还有其他各种形状的, 比如矩形、V形、Y形、C形、H形等等. 比如V形, 可能通过V的两臂之间的夹角可以改变相位, C形则可能是旋转开口方向.

然后按照自己需要产生的相位变化, 把这些小天线整齐摆放好, 就成了神奇的光学元件.

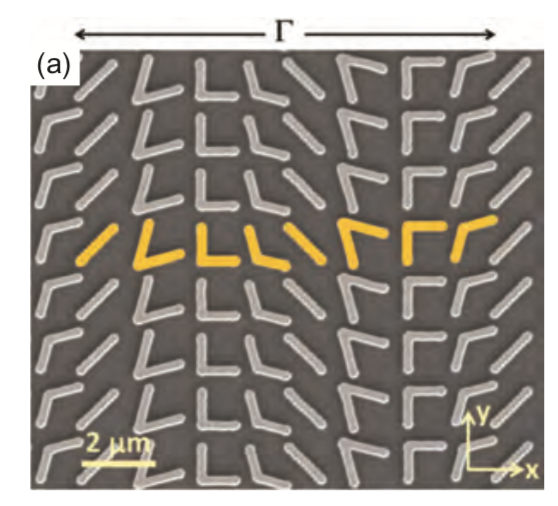
比如把C形天线的方向依次线性旋转, 就可以得到一个棱镜, 而如果旋转过程是x^2的, 那么就可以得到一个透镜了.

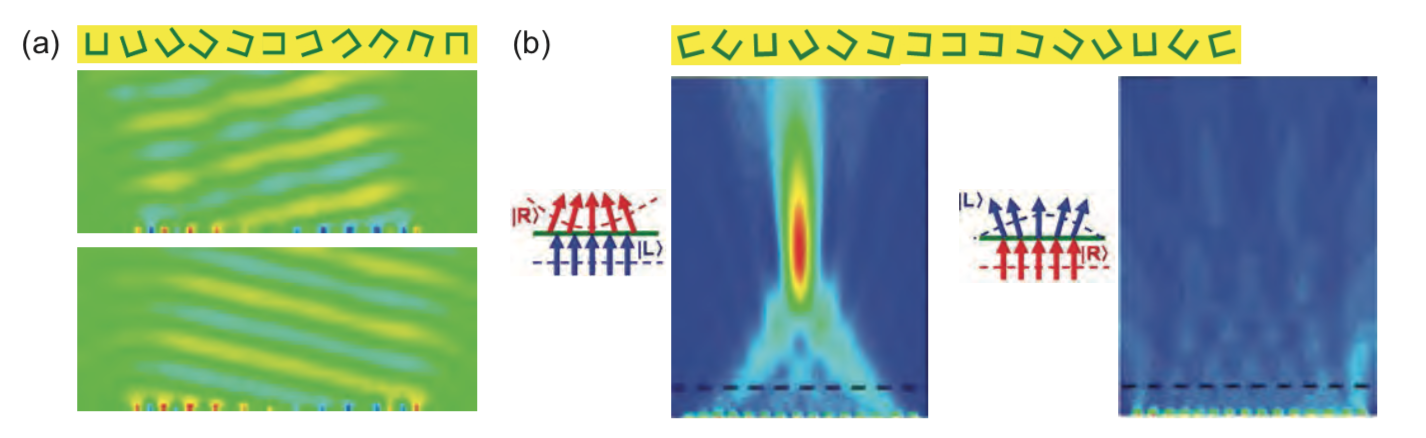
这些小天线的尺度, 每个大约是半波长左右, 如果是可见光, 那么就是400-700nm的一半, 也就是200nm-350nm左右. 要用光刻的方法加工了. 但想想现在的芯片都是7nm、十几纳米的加工工艺了, 几百纳米的光刻是很久以前就能够达成的技术了.

对于波长更长的电磁波, 比如红外、微波、无线电波, 制造天线还更容易一些. 甚至用金属3D打印就有可能.

对于可见光, 这种透镜是超薄的, 都到不了毫米的厚度, 而且没有球差之类的问题.

关于各种魔法特性和局限性, 将在下一部分讲解. 未完待续.

参考链接