第一门课第二周, 主要讲

各种率¶

• 真假阴阳各种率
• 敏感性和特异性
• 阳性预测率(PPV)和阴性预测率
• 置信区间, ROC曲线, F1 score

我之前学Scikit-learn的时候, 笔记记得挺清楚的.

参考

• Scikit-learn笔记2
• Scikit-learn笔记3
• Scikit-learn笔记4

而且这张图做得很好, 一张图说明问题, 先看图, 再看后面的计算方式:

例如有这样的结果:

	预测=A	预测=B	预测=C
实际=A	100	6	11
实际=B	1	110	12
实际=C	2	7	120

以下表格中, 分子是红字, 分母是黄色背景, 考虑C的情况

Accuracy¶

• 正确率
• 有病没病都说对了的概率

	预测=A	预测=B	预测=C
实际=A	100	6	11
实际=B	1	110	12
实际=C	2	7	120

$$ Accuracy=\frac{100+110+120}{100+6+11+1+110+12+2+7+120} $$

---

Recall¶

• 敏感性, 检出率, 真阳性率.
• 实际有病, 测出有病的概率

	预测=A	预测=B	预测=C
实际=A	100	6	11
实际=B	1	110	12
实际=C	2	7	120

$$ Recall=\frac{120}{2+7+120} $$

---

Precision¶

• 精确度, 阳性预测率, PPV
• 测出有病, 还说对了的概率

	预测=A	预测=B	预测=C
实际=A	100	6	11
实际=B	1	110	12
实际=C	2	7	120

$$ Precision=\frac{120}{11+12+120} $$

---

Specificity¶

• 特异性, 真阴性率
• 测出没病, 还说对了的概率

	预测=A	预测=B	预测=C
实际=A	100	6	11
实际=B	1	110	12
实际=C	2	7	120

$$ Specificity=\frac{100+6+1+110}{100+6+1+110+2+7} $$

---

False Positive Rate¶

• 假阳性率, 误报率
• 本来没病, 测出有病的概率

	预测=A	预测=B	预测=C
实际=A	100	6	11
实际=B	1	110	12
实际=C	2	7	120

$$ False Positive Rate=\frac{11+12}{100+6+11+1+110+12} $$

---

真假阴阳性¶

	预测为(-)	预测为(+)
实际为(-)	TN	FP
实际为(+)	FN	TP

• TP = true positive 真阳性
• FP = false positive (Type I error) 假阳性(Type I错误) , 印象里就是P<0.05的0.05
• TN = true negative 真阴性
• FN = false negative (Type II error)假阴性(Type II错误)

敏感特异性¶

• Accuracy: 分类正确的概率. 实际为(-)预测为(-), 实际为(+)预测为(+)叫做正确. $$ Accuracy=\frac{TP + TN}{TP + TN + FP + FN} $$

• Classification error: (1-Accuracy), 分类错误的概率 $$ Classification\; error=\frac{FP + FN}{TP + TN + FP + FN} $$

• Recall, 真阳性率: 实际上为(+), 能够被预测成(+)的概率

  • Recall又叫
  • True Positive Rate (TPR): 真阳性率
  • Sensitivity: 敏感性
  • Probability of detection: 检出率 $$ Recall=\frac{TP}{TP+FN} $$

• Precision: 如果预测为(+), 那么预测正确的概率 $$ Precision=\frac{TP}{TP+FP} $$

• False positive rate (FPR): 假阳性率, 误报率. 本来实际上是(-)的, 结果分类器报告成(+)的概率

$$ False Positive Rate=\frac{FP}{TN+FP} $$

• Specificity, 特异性

应该是真阴性率(之前写错了), TNR, 实际上为(-), 能够被测成(-)的概率 $$ Specificity=\frac{TN}{TN+FN} $$

F1-score: 结合precision与recall¶

$$ F_1=2\frac{precision \times recall}{precision+recall}=\frac{2TP}{2TP+FN+FP} $$

F-score: 更一般地将precision与recall结合成单独一个数¶

$$ F_\beta=(1+\beta^2)\frac{precision \times recall}{\beta^2\times precision+recall}=\frac{(1+\beta^2)TP}{(1+\beta^2)TP+FN+FP} $$

𝛽用来调整recall vs precision之间的重要程度:

• Precision-oriented users: 𝜷 = 0.5
• Recall-oriented users: 𝜷 = 2

阳性预测率 PPV¶

实际上就是

• Precision: 如果预测为(+), 那么预测正确的概率 $$ Precision=\frac{TP}{TP+FP} $$

$$ PPV = Precision = \frac{sensitivity \times prevalence}{sensitivity \times prevalence+(1 - specificity) \times (1 - prevalence)} $$

其中 prevalence=P(pos), 阳性结果的发生率. 如果自己都知道TP、FP的数据, 当然用简单的公式计算, 如果拿到的是一个标记好各种率的试剂盒, 或者是看一篇新闻报道, 对方把各种率搅合在一起, 那么可能就要通过后一种公式来计算

置信区间¶

比如某个概率p=0.80(95% CI 0.78, 0.82),

是说, 真实的概率p, 谁知道是啥, 有95%的概率, 会落在[0.78, 0.82]的范围内. 置信区间的范围和样本量有关, 样本量越大, 置信区间的宽度越窄.

ROC曲线¶

• X轴: False Positive Rate 假阳性率
• Y轴: True Positive Rate 真阳性率

左上顶点:

• 理想点
• False positive rate 假阳性率=0
• True positive rate 真阳性率=1

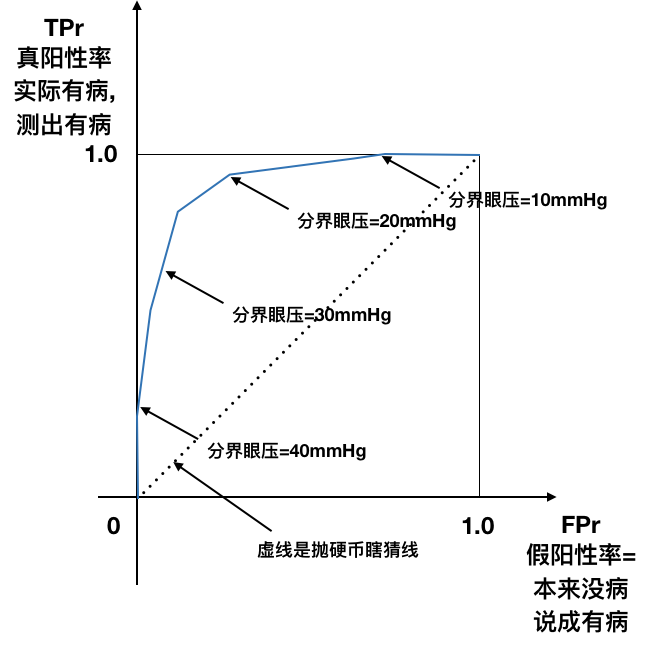
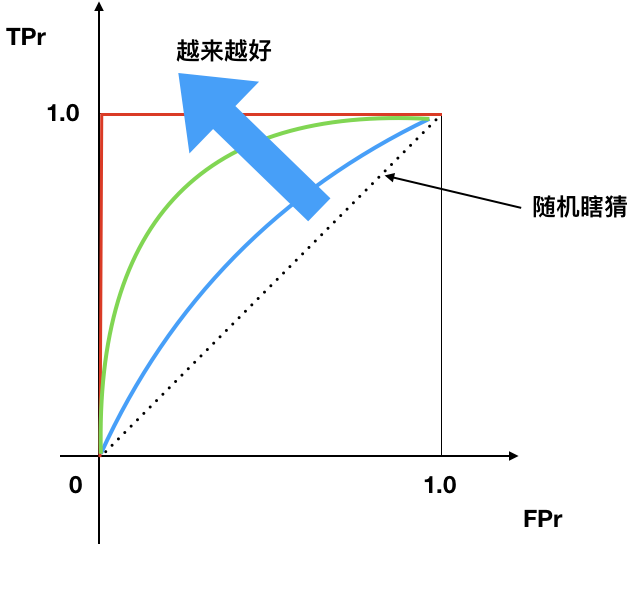
• ROC曲线越往左上, 越好.
• 曲线下面积(AUC), 越大越好
• 45度线是随机瞎猜线