专利分析工具概述(0)

最近偶遇一个专利分析班, 在图书馆闲逛时偶遇的. 图书馆是一个偶遇好书、好课的地方.

学完课程之后, 意犹未尽. 搜索时发现了世界知识产权组织(WIPO)推出过一个WIPO开源专利分析手册 内容非常好, 而且也是开源发布的. 所以就想顺手给翻译了.

这里先捡重要的部分翻译先. 其中的第二章 工具概述 里介绍了大量的专利分析工具, 这些工具不仅在专利分析, 在其他数据分析领域看起来也会很有用.

于是先翻译之.

该手册写于2016年, 其中有些外链的链接可能已经改变或者失效. 我会在翻译时尽量查找, 但也可能有所疏漏.

阅读更多…

看好和弦学音乐和sonic-pi

Sonic-Pi是一个用Ruby语言写的音乐编程工具, 可以使用代码来即兴“演奏”音乐. 所谓演奏,live coding music, 是可以在程序中修改代码, 随时更新, 使音乐发生变化. 有点像是用命令行的DJ. 比如这个演出

不过学习Sonic-Pi就有两个内容要学习了, 一个是Ruby语言, 一个是音乐语言.

  • Ruby语言

    • Sonic-Pi本身使用的是Ruby语言, 用来编写音乐的也是Ruby的一个子集, Sonic-Pi自带的mehackit上有个快速上手的中文教程, 文字阅读困难的, 这里也有视频教程
    • 如果需要更复杂的功能, 可能需要加强Ruby语言的学习, 引入更多数据结构、函数定义之类. Ruby是个很流行的语言, 有大量的教程可以参考, 比如30分钟的快速入门 或者更完全一些的教程
    • 对于Sonic-Pi, 简单的音乐或者midi处理, 似乎还用不到面向对象编程, 多数是面向过程的, 如果会其他的编程语言, 很容易学会.

  • 音乐语言

    • 音乐语言就要复杂多了, 概括地说音乐只是模式涌现. 但为了让人类的大脑觉得好听, 还有很多的规律.
    • 很多“学习音乐”的人, 比如我小时候学琴, 只是学习了乐器的演奏, 并没有学习用音乐来表达. 学习演奏类似于学习写字, 高等一点的类似于学习书法. 音乐则是类似文学, 至少要有一些写作的训练才行, 也就是乐理的学习.

好和弦(NiceChord)是一个台湾作曲家做的“作曲、編曲、即興和電腦音樂的 YouTube 教學頻道”, 从2014年到现在已经更新了200多集了. 每一集5-10分钟, 轻松有趣. 是很好的乐理课程.

既然我同时在学习这两者, 我就干脆结合在一起学. 所以我对着好和弦的课程, 尽量给每一集写一段对应的Sonic-Pi代码. 目前写了10集左右, 如果我不太懒的话, 就持续更新.

您可以将代码贴到sonic-pi的编辑器里然后运行, 就可以听到结果了. 推荐顺手改改其中的代码, 也许能够产生更好的效果.

其中也有很多比较固定的音乐表达方式, 比如常用的和弦琶音生成、12小节蓝调. 我还可能会加入一些自己会的编程技巧, 比如马尔可夫链、状态转移之类.

这些代码供抛砖引玉, 您可以直接拿到自己的sonic-pi音乐中.

项目地址: https://github.com/goldengrape/sonic_pi_for_nice_chord

音乐编程

一个月前我买了一件电子乐器artiphon instrument1, 然后就沉迷于音乐不能自拔.

sonic-pi

前几天重新翻看好和弦, 其中有一集说到用各种开源或者免费的软件制作音乐, 里面提到了sonic-pi, 说可以用写程序的方法做现场音乐演出.

于是我就去下载了sonic-pi来玩, 确实很有趣. 可以play音符, 可以播放采样(sample), 也就是事先录制好的声音, 可以循环播放一组音符或者声音, 于是就有节拍、和弦, 还可以引入随机数, 可以产生变化的旋律. 还可以和midi硬件交互.

我写了一段代码, 可以将我的artiphon instrument1 中的特别低的低音(反正平时很少用到), 映射到和弦上, 于是我就可以用一个键来演奏需要好几个手指扭来扭去才能弹出的和弦了.代码

我开始以为这只是一个专门用来写音乐的语言, 随着学习的深入. 怎么看到了越来越多的编程内容, 数组、分支、循环甚至函数. 看完了基础教程以后, 感觉这就是个图灵完备的计算机语言啊. 搜索了一下sonic-pi的来历, 果然, 其实sonic-pi是Ruby语言的一个方言. 没想到我为了弹吉他偷懒, 居然顺手学了一多半Ruby.

Live Coding Music

我对音乐编程更有兴趣了. 在github上搜了一下, 发现这个Awesome Live Coding Music的列表.

大名鼎鼎的潮流解释型语言一网打尽呐, 艺术家们果然是技术先行者.

感觉Live Coding Music非常适合儿童(/中老年)编程教育,

  • 语法循序渐进,
  • 从语法上, play声音的命令远远比print、cout要有趣得多, 又比画个GUI简单得多.
  • 变量命名时, 音符本来就有do/re/mi,CDE, 123, 几类名字混在一起, 所以对变量应该比较容易理解.
  • loop和循环天然对应.
  • 函数/块完全是复用性出发.
  • 多乐器、多音轨天然对应多线程.
  • 还有众多midi硬件、通讯问题
  • 写出来的东西很容易出成就感
  • sonic-pi的口号是“没有错误, 只有机会”, 用在编程学习上, 不容易出现挫折感. 音乐这种东西, 规律出现了就不会太难听.
  • 编程的结果是产生音乐, 可以录制成wav、mp3文件, 很容易分享. 即使在别人没有安装什么额外软件的条件下, 也可以播放成果. 当然也可以放在soundcloud这样的音乐作品分享网站上. 比如我按照好和弦的指导做的这首伴奏. 炫耀是互联网第一生产力, 也可以用来督促学习.
  • 编程技巧上, live coding对程序需求的修改又是大量、即时的, 演奏者自己就是个不断改需求的甲方, 所以慢慢各种编程技巧都会自然加入. 为了快速切换风格, 很可能要准备上各种设计模式.

所以等我学完了Ruby(sonic-pi), 考虑把Clojure和一直没啃下来的JavaScript通过音乐来搞定.

对冲式学习

  • 我最近学习弹吉他, 为了偷懒学会了Ruby,
  • 我之前想研究书法的用笔, 虽然没搞定写书法的机械臂, 却好好练习了书法.
  • 再往远想, 我高中时就是用Mathematica(那时候还是4.0, 现在都12了)写数学和物理作业.

所以可以引入“对冲式学习”的概念: 同时学习两个东西, 互补没学好的风险, 其中:

  • 一个是古老的对技巧要求很高的技艺, 比如乐器、书法、解数学物理题;
  • 一个是现代的可自动重复的工具, 有可能降低前者的难度, 比如音乐编程、CNC、mathematica.

两者同时学习, 反正学会其中一个就很有收获, 也可能慢慢两者都会了.

人工晶体度数计算公式推导(2)

考虑到Olsen T那篇综述后面基本是在吐槽, 没有继续讨论具体公式的推导. 所以我换一篇文献, 这次看的是Barrett Universal公式的初始形态, Intraocular lens calculation formulas for new intraocular lens implants80037-8)

1987年的Graham D. Barrett, M. D.还是一位具有分享精神并且自己会写GW Basic的青年. 不像现在这么吝啬, 满世界也翻不到他的Barrett Universal II和Barrett True K公式的解析形式, 只有网页上才有计算器.

眼科医生保有“公式的手算能力”是非常重要的, 谁知道哪个程序员会不会把毫米和米弄混, 把某个参数和另一个参数搞错? 真弄明白的时候都是大规模回顾数据的时候, 那时人工晶体早在眼内稳定好多年了.

大概那个乐于分享的时代快要逝去了吧.

Barrett Universal公式是基于Gaussian optical principals的, 是基于计算厚透镜用的公式, 于上集见到的薄透镜公式有所不同. 这里要考虑透镜的厚度, 还要考虑厚透镜的主平面

Fig3

In [ ]:

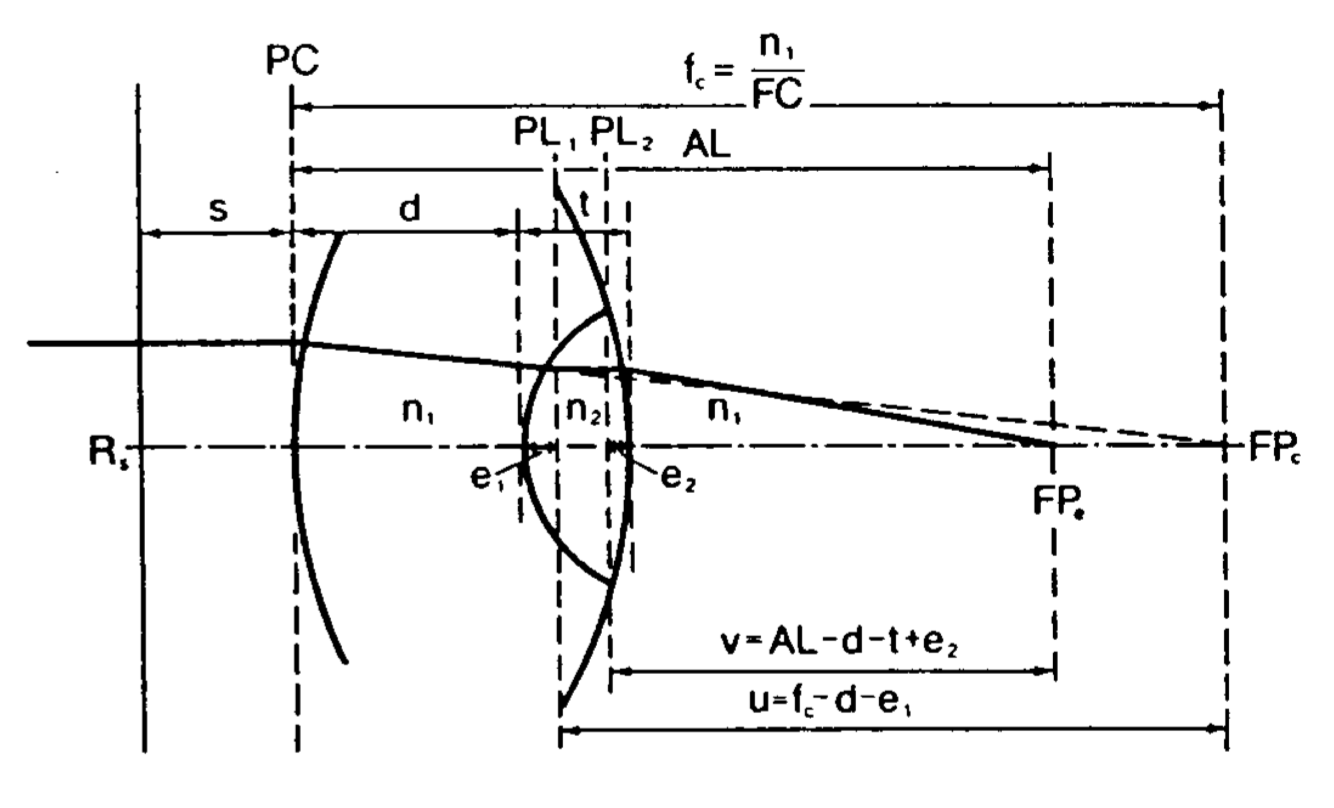
示意图看起来很复杂, 一点一点解释:

人工晶体就是中间的那个, Barrett当时是为了给水凝胶晶体推导公式, 所以人工晶体的长相比较奇怪. 设定人工晶体的厚度是t, 折射率是$n_2$, 人工晶体的前表面距离角膜顶点为d.

人工晶体前表面的屈光度是$FP_1$, 后表面的屈光度是$FP_2$, 接下来两个参数$e_1, e_2$要稍微解释下

回忆一下中学光学作图的时候, 画出一个薄透镜折射时, 我们只需要用一条直线代替透镜, 然后画出平行光与这个直线相交的点. 也就是把透镜当作一个没有厚度的平面来处理.

对于厚透镜, 要考虑前后两个面, 但这两个面的位置并不是紧贴着前后表面的顶点, 而是离开一点距离, 这两个面称为Principal Plane, 与光轴的交点成为Principal Point(主点).

Principal Plane, 是把入射光和出射光各自的延长线相交, 得到的平面. (补插图)

示意图中的$e_1, e_2$就是前后Principal Plane到透镜实际顶点之间的距离.

S是眼镜到角膜之间的距离, 眼镜度数Rs就是验光得到的结果, 角膜的屈光度是K

$$ FC=K+\frac{Rs}{1-S \times Rs} \tag 1 $$
In [ ]: