EDoF综述翻译

源文件

今天查文献，看了一篇扩展焦深(Extended Depth of Foucs, EDoF)的综述。

Zeev Zalevsky "Extended depth of focus imaging: a review," SPIE Reviews 1(1), 018001 (1 January 2010). https://doi.org/10.1117/6.0000001

感觉不错，部分翻译之。

全文在SPIE的数据库中

按眼科习惯，pupil翻译成了瞳孔

Extended depth of focus imaging: a review

Zeev Zalevsky

Bar-Ilan University, School of Engineering, Ramat-Gan, 52900, Israel

zalevsz@eng.biu.ac.il

1 理论背景

光学成像系统达到较高的横向分辨率范围，称为焦深（Depth of Focus）或者景深（Depth of Field），具体使用那个名称取决于是在像空间还是在物空间描述。 从波动光学的角度来看，由于离焦在系统光瞳函数中引入了额外的二次相位，导致空间低通滤波效应，从而产生有限的焦深。 这种效应可以用系统的光学传递函数 (OTF) 均值H(μx, μy)来描述. 单透镜成像系统的光学传递函数可以表示为适当比例的透镜瞳孔函数的自相关 P(x, y) [1]:

$$ H\left(\mu_{x}, \mu_{y}\right)=\frac{\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} P\left(x+\frac{\lambda Z_{i} \mu_{x}}{2}, y+\frac{\lambda Z_{i} \mu_{y}}{2}\right) P^{*}\left(x-\frac{\lambda Z_{i} \mu_{x}}{2}, y-\frac{\lambda Z_{i} \mu_{y}}{2}\right) \mathrm{d} x \mathrm{d} y}{\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}|P(x, y)|^{2} \mathrm{d} x \mathrm{d} y} \tag{1} $$

其中 λ 是光波长，μx, μy 是空间频率，和 Zi 是镜头到像平面的距离。对于圆形瞳孔，在没有像差的情况下，P(x, y）由二元圆瞳孔函数给出，其等于瞳孔内 1，瞳孔外 0。在这种情况下，OTF 可以简单地写为

$$ H\left(\mu_{x}, \mu_{y}\right)=\frac{\text { Area of overlap }}{\text { Total area }}=\frac{\iint_{A\left(\mu_{x}, \mu_{y}\right)} \mathrm{d} x \mathrm{d} y}{\iint_{A(0,0)} \mathrm{d} x \mathrm{d} y} \tag{2} $$

其中 A(μx,μy)给出两个移位瞳孔之间的重叠区域【有卷积运算，所以其实是相当于把一个圆在另一个圆上移动，取得重叠区域的面积，即为结果，译者注】，A(0,0)是瞳孔的总面积。当引入像差时，广义瞳孔函数的形式

$$ P(x, y)=|P(x, y)| \exp [i k W(x, y)] \tag{3} $$

其中 W(x,y）为波像差函数和 k=2π/λ。下面就是在离焦的情况下，W(x,y）的二次函数形式：

$$ W(x, y)=W_{m} \frac{\left(x^{2}+y^{2}\right)}{b^{2}} \tag{4} $$

其中 b 孔径的半径。系数 Wm 确定离焦像差的严重程度，公式如下：

$$ W_{m}=\frac{\Psi \lambda}{2 \pi} \tag{5} $$

其中 ψ 定义如下

$$ \Psi=\frac{\pi b^{2}}{\lambda}\left(\frac{1}{Z_{i}}+\frac{1}{Z_{o}}-\frac{1}{f}\right) \tag{6} $$

其中，Zo是从物体到镜头的距离，f是透镜的焦距。当满足成像条件时：

$$ \frac{1}{Z_{i}}+\frac{1}{Z_{o}}=\frac{1}{f} \tag{7} $$

并且畸变因子 ψ 等于零。当成像条件不满足时，公式(3)(4)的二次相位因子导致 OTF 分布变窄，即产生低通效应或者说抑制了较高的空间频率含量。对于一维的情况，公式(1)变形为：

$$ \begin{aligned} H\left(\mu, W_{m}\right) &=\frac{\int_{-\infty}^{\infty} P\left(x+\frac{\lambda Z_{i} \mu}{2}\right) P^{*}\left(x-\frac{\lambda Z_{i} \mu}{2}\right) \mathrm{d} x}{\int_{-\infty}^{\infty}|P(x)|^{2} \mathrm{d} x} \\ &=\frac{\int_{A(\mu)} \exp \left[\frac{i k W_{m} \lambda Z_{i} \mu x}{b^{2}}\right] \mathrm{d} x}{2 b} \end{aligned} \tag{8} $$

其中 A(μ）是两个移位瞳孔函数之间的一维重叠。解公式(8)，得出 1-D OTF：

$$ H(\mu)=\left(1-\frac{|\mu|}{2 \mu_{\mathrm{c.o.}}}\right) \operatorname{sinc}\left\{\frac{8 W_{m} \pi}{\lambda}\left(\frac{\mu}{2 \mu_{\mathrm{c.o.}}}\right)\left(1-\frac{\mu}{2 \mu_{\mathrm{c.o.}}}\right)\right\} \tag{9} $$

其中$\mu_{\mathrm{c.o.}}=\frac{b}{\lambda Z_{i}}$，此表达式用于 H (μ）可近似为

$$ \begin{aligned} H(\mu) & \approx \frac{\int_{A(0)} \exp \left[\frac{i k W_{m} 2 \lambda Z_{i} \mu x}{b^{2}}\right] \mathrm{d} x}{2 b} \\ &=\frac{\int_{-b}^{b} \exp \left[\frac{4 \pi i W_{m} Z_{i} \mu x}{b^{2}}\right] \mathrm{d} x}{2 b} \\ &=\frac{1}{2 b} \cdot \int_{-\infty}^{\infty} \operatorname{rect}\left(\frac{x}{2 b}\right) \exp \left[\frac{4 \pi i W_{m} Z_{i} \mu x}{b^{2}}\right] \mathrm{d} x \\ &=\operatorname{sinc}\left(\frac{4 W_{m} \pi \mu Z_{i}}{b}\right) \end{aligned} \tag{10} $$

图1

该近似值应满足以下条件: μ与$\frac{b}{\lambda Z_{i}}$ 相比不算太大，这样，A(μ）可近似为镜片的面积A(0)。该近似值也适用于 Wm值很大，导致指数的参数快速振荡。公式(10)显示了空间低通滤波效果。

在二维圆孔的情况下，得到了只有径向频率依赖性的OTF，在参考文献2中有推导。它被表示为一个Jn的级数展开，例如第一种类型的贝塞尔函数的第n项。

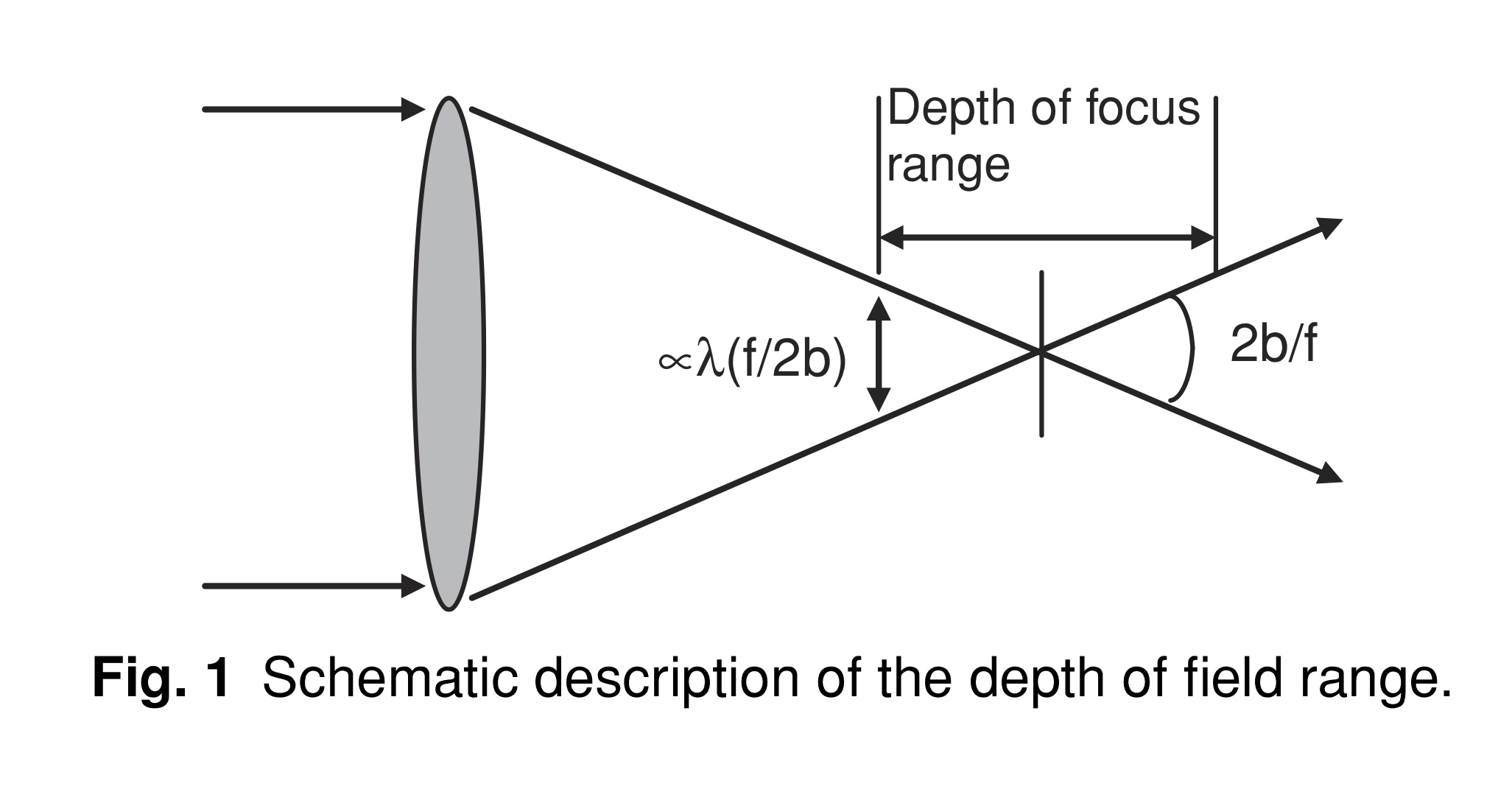
如果希望估计焦深，则很容易证明焦深与波长和F数平方的乘积近似成正比。（F数，焦距与成像透镜直径的比值），即 $\lambda(f/2b)^2$. 从图1中很容易看出原因。由于衍射极限分辨率限制与 λ(f/2b）（点扩散函数的维数）成正比，光束发散时的几何角度为（2b）/f，那么得到的离焦光斑等于景深范围，乘以角度（2b）/f，并且应与 λ(f/2b) 成正比. 从这个关系式可以得出这样的结论：焦深范围正比于$\lambda (f /2b)^2$.

2 概述：扩展景深的方法

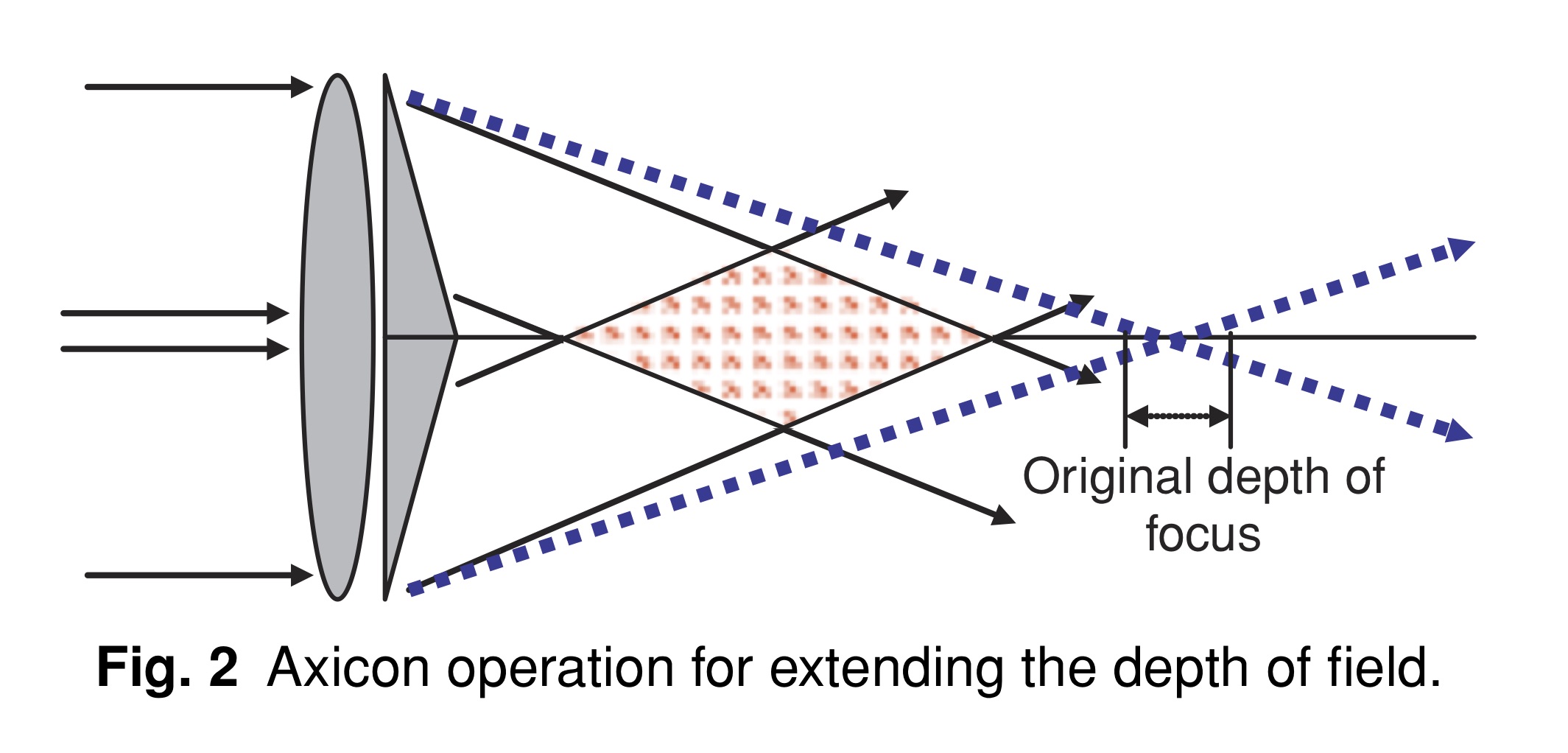
随着摄影技术的发展，研究了各种方法来克服第一部分中描述的离焦限制。 最简单的方法是简单地减小成像镜头的孔径。减少可能是渐进的，例如在孔径切趾【在瞳孔边缘以模糊渐变来“切除”点扩散函数的“脚趾”，译者注】，或突变的，通过在孔径平面增加二进制阻塞/传输掩模 [3,4]. 不幸的是，更小的孔径降低了系统分辨率。（使公式(1)中的OTF更窄），也会减少到达影像平面的通光量。因此研发了其他一些办法。一种解决方案是在成像系统的孔径中增加折射元件。最流行的元素之一是 axicon[5,6]. 该元件的工作原理如图2所示。在轴棱锥偏转光束的交叠区域，用图中的虚线表示，得到扩展景深 (EDOF) 区域。为便于比较，蓝色虚线表示不存在 axicon 时的原始光线跟踪。

图2

另一种基于折射元件的解决方案涉及多个透镜的多路复用，每个透镜具有不同的焦距。空间复用的一个例子是在“渐进式”或多焦点眼镜（如双焦点 [7] 或多焦点镜片 [8,9]). 在这些透镜中，两个（或更多）焦距在空间上是分开的，只允许在小部分视场内实现所需的聚焦性能。不同的透镜划分透镜光阑的平面，因此，由于每个透镜只覆盖光阑的有限部分，

系统具有较大的有效f数，从而降低了分辨率。另一方面，如果应用是眼镜，那么这样的解决方案就会限制视野，因为为了选择焦距以便聚焦到所需的距离，需要选择合适的视线。

一种不同的复用方式是几个镜头通过编码复用。在这种方法中，具有不同焦距的复用透镜被分成非常小的片，这些片随机散布在整个孔径平面上。这类解决方案通常是指多个衍射透镜。每个镜头覆盖全光瞳，因此每个镜头的分辨率不会降低 [10–12]. 这种编码复用可以通过随机地分布透镜或者通过在整个光阑平面上周期性展开每个透镜来实现。由于多片透镜的多路复用，孔径平面上密集的空间变化，很大一部分光能量通过大角度衍射转移。其结果是降低能量效率和眩光效应。与所有基于衍射的方案一样，由于衍射透镜的焦距与波长有关，因此系统表现出显著的色差。

另一种 EDOF 技术采用连接到成像透镜的立方位相元件 [13]. 这个想法基本上是插入比离焦像差更强的像差，这样通过数字后处理就可以重建出清晰的图像。与之前的方法相比，这种类型的解决方案不是全光学方法，而是需要数字后处理，因此不适合眼科（即视力矫正）应用。其他有趣的孔径编码技术需要数字后处理讨论在参考文献[13–15] 以及参考文献16中的镜片切趾技术。其他相关技术包括用分数阶相位板剪裁调制传递函数 [17] 和对数非球面透镜 [18].【这俩是啥？译者问】

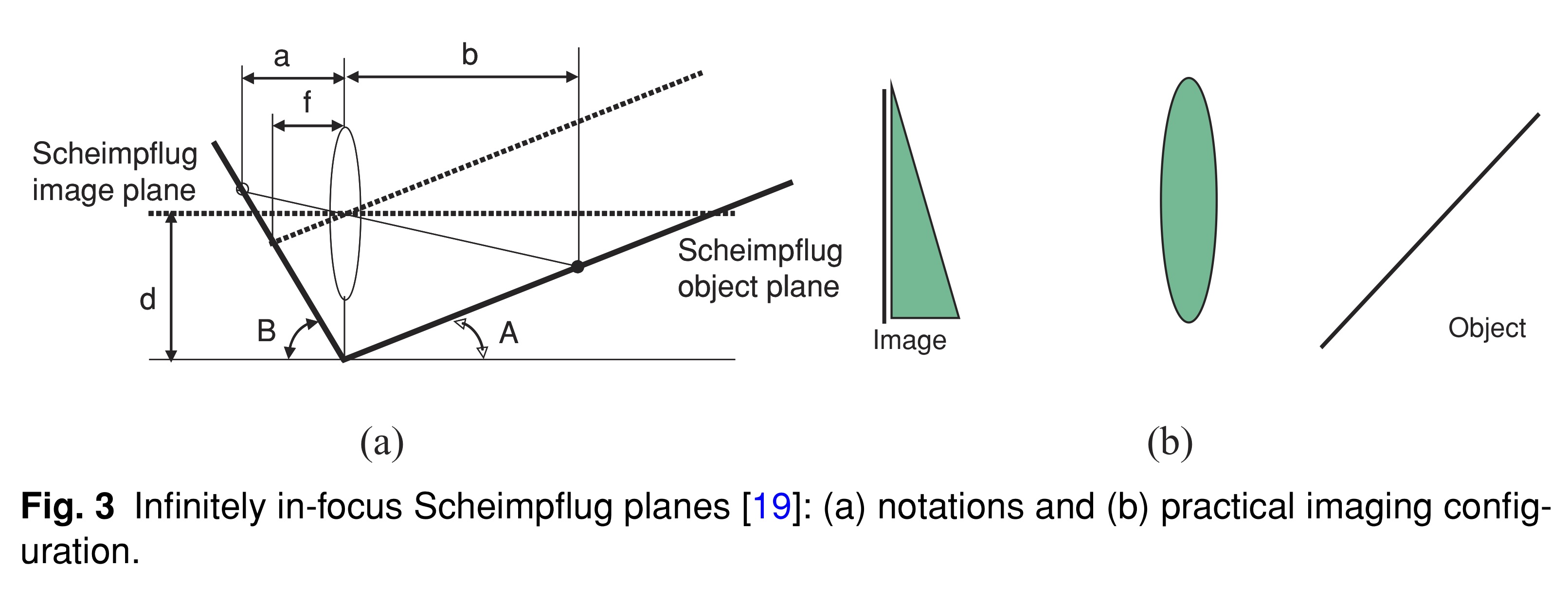
一个不同的和历史上重要的扩展景深的方法涉及 Scheimpflug[19]，他通过重新定位成像系统提供的理论上可以无限扩展焦深。Scheimpflug设置的示意图见图3(a)， 及其在实际光学中的实现方式见图3(b)

在此配置中，必须满足以下数学条件：

$$ \frac{1}{a}+\frac{1}{b}=\frac{1}{d}(\tan B+\tan A)=\frac{1}{f} \tag{11} $$

Scheimpflug成像中，图3(a)中指定的线上物和像始终对焦清晰，因此沿这些平面定位的物体将始终成像于焦点上。这种方法的主要缺点是，在“渐进”镜片的情况下，视野非常有限，因为每个轴向距离都在不同的侧位成像。

图3

近年来出现了几种新的全光聚焦方法。这些方法的发展不仅对照相机的数字成像非常重要，而且对眼科视力矫正也非常重要。在一种方法中，焦深通过增加多个衍射环来扩展[20]。如前所述，使用衍射元件的一个缺点是伴随的色差。另一种方法，更多的是折射型，因此表现出减少的色差，包括一个由环组成的非二元剖面，这些环加在孔径透镜顶部，以产生穿过孔径的不平衡光程差[21] 【待研究，译者注】

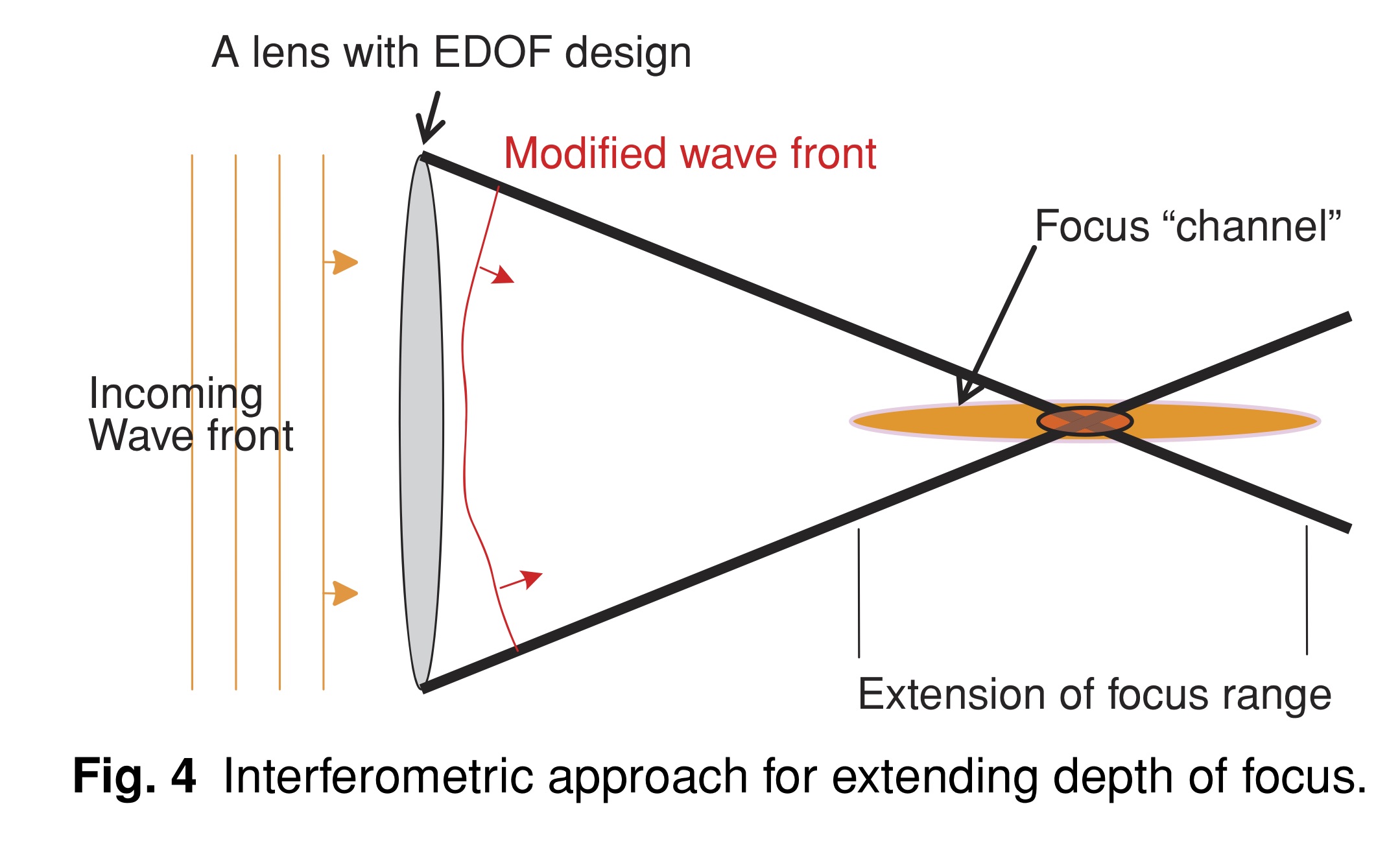
一个不同的全光学方向提供了一个基于干涉而不是衍射/折射类型的解决方案，见参考文献中[22]和[23]. 其基本思想是将成像透镜视为干涉仪中的一个部件。这样的解释是可能的，因为在焦点位置所有通过光阑的光线被叠加加起来。 通过在成像透镜顶部适当增加光学相位雕刻，在“焦点通道”中产生所需的建设性干扰，同时在其周围产生破坏性干扰（见图4). 添加的轮廓本身没有光学能力，但必须与成像透镜结合使用。光学轮廓雕刻具有较大的空间特征，因此不是衍射型元件。其蚀刻深度很小（约 1 μm），因此不会像在折射方案中那样增加物理路径差异【似乎不是在说光程差？译者注】。由于这种方法能量效率更高，并且表现出色差降低，因此适合眼科应用。 【参考文献22，23要重点看看，译者关注中】

图4

另一种扩展景深的全光技术是使用双折射透镜。最近，提出了一种新的方法，制作了一个双折射透镜 [24] 具有两种焦距，一种用于普通偏振态，另一种用于非常偏振态。它是一种单焦透镜，由于制造它的材料的双折射而变成双焦透镜。通过对透镜的适当设计，可以选择两个焦距，使聚焦范围扩大到大约两倍的焦深 [25]. 然而，制作这样的透镜是复杂和昂贵的。显然，这种工作原理只适用于外部照明没有偏振的情况，允许照明能量在两个焦点之间分配。一种简化的解决方案包括使用常规单焦点透镜并在透镜和成像平面之间添加双折射板 [26]. 板的增加为两个偏振产生不同的光路，因此每个偏振与单焦点成像透镜的聚焦距离不同。假设自由空间中所需光程差为$\Delta$，双折射材料具有普通和特殊的折射率分别为 $n_o$和 $n_e$，则双折射板的宽度应为：

$$ \Delta_{B}=\frac{\Delta}{\left(1-\frac{n_{0}}{n_{\mathrm{e}}}\right)} \tag{12} $$

注意，最后一个方程对于入射光束的垂直入射是有效的，并且非垂直入射角（主要对应于视场的边缘）不会得到合适的焦深扩展。

如前所述，使用针孔降低了分辨率和能量效率，但显著增加了系统的景深。因此，实现焦深扩展的一个可能的改进是使用随机针孔板代替成像透镜。[27,28]. 在这种情况下，能量效率是提高的，因为有许多针孔覆盖镜头光圈。分辨率虽然降低，但可以通过适当的数字滤波操作恢复。这种结构的一个很好的特点是，由于针孔掩模是随机的，OTF 具有随距离变化的随机相位分布。因此，可以通过适当校正 OTF 的相位来提取到图像中各种物体的距离。每次相位校正都将导致焦点内物体定位在不同的轴向距离上。如果考虑数字后处理，则可通过观察傅里叶平面中产生的零点，从图像以数字方式估计离焦量[29,30].

扩展景深主题与波束成形密切相关，为此目的采用的方法与本综述相关。基于 Gerchberg–Saxton 的迭代算法[31,32]以及解析优化3D点扩散函数的方法[33]，已被证明在正确设计点扩散函数时是有用的。控制点扩展函数的三维形状可以用来进行波束成形和扩展焦深。优化过程可以通过基于广义传播不变波场的描述 [34,35] 或通过使用变分法的 3-D 优化 [36,37]. 所需的波束整形也可以通过成像透镜孔径的适当相位和振幅切趾获得，如参考文献[38–42]所述。在参考文献[41]中，作者介绍了如何利用傅里叶变换工具获得的光学系统的光瞳函数来调整系统的焦深。【这篇要看看，译者想】

3 老视与人类视觉

【这一部分看起来比较陈旧，翻译略】，提到可能可以用EDoF来阻止儿童近视进展。

4 结论

略

参考文献

见原文

In [ ]: