一千零一个病人¶

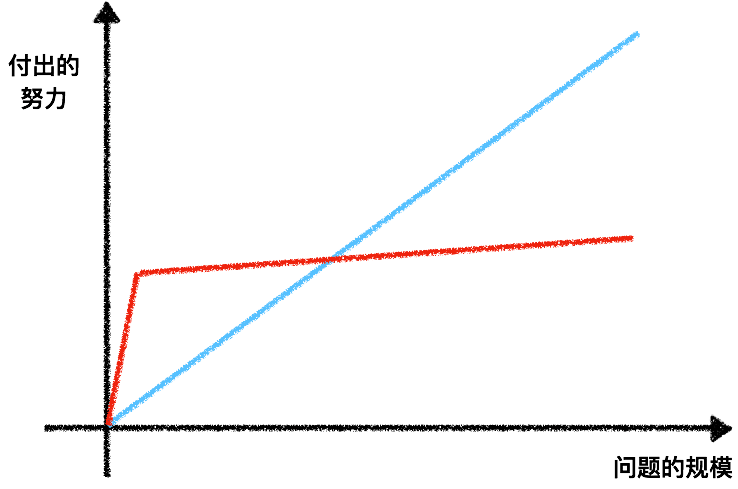
普通人干活往往是图中蓝色的曲线, 随着问题规模的增长, 付出的努力或者工作量也随之线性增长. Nerd, Geek这类人干活则是红色的曲线, 当他们遇到一个可能反复出现的问题时, 先要花大力气去搞出一个自动化的东西, 然后不论问题再怎么增长规模, 他们也只不过是跑跑自动化的工具, 不费什么力气. 这就是编写程序的意义所在.

之前我们写了计算IOL度数的程序似乎没有什么意义. 每计算一次都还要敲上print, 再调用函数. 看起来并不必手工或者用IOL master之类的机器好多少.

不过如果现在是个临床研究, 一下子要处理上1001个病人的数据, 用上不同的公式来计算他们所需的IOL度数, 再和术后3个月的验光结果比较. 看哪个公式的预测最准确, 那手工再输入到IOL Master里面一个一个算就复杂了.

产生多人数据¶

下面我们要使用numpy这个工具包来产生多个随机数据, 来模拟很多人的情况, 为了方便显示, 只是产生5个人的数据好了.

import numpy as np
np.random.seed(0)

patient_number=5
L=np.random.rand(patient_number,1)*4+23
K_1=np.random.rand(patient_number,1)*2+40
K_2=np.random.rand(patient_number,1)*2+41
REF=np.round(np.random.rand(patient_number,1))*(-3)
A=np.random.choice([118.4,119.0,118.0],size=(patient_number,1))
print(L)
print(A)

[[ 25.19525402]
 [ 25.86075747]
 [ 25.4110535 ]
 [ 25.17953273]
 [ 24.6946192 ]]
[[ 118. ]
 [ 118.4]
 [ 119. ]
 [ 119. ]
 [ 118. ]]

import numpy as np

之前已经讲解过了, 就是导入numpy这个科学计算工具包, 并且简称为np, 那么Numpy工具包里面的函数, 就用np.函数名来表示了.

如果在上面有错误, 在导入numpy时出错, 请确认是在coclac里使用的kernel是python3(anaconda)

但具体应该用什么函数来实现需要的功能, numpy的函数在撰写上有什么要求, 就需要查numpy的手册了: https://docs.scipy.org/doc/numpy/reference/ 更简单一些的, 我们可以直接去搜索去搜索, 这也是我接下来要讲的:

面向Google/ StackOverFlow的编程¶

一切有现成答案的问题, 都可以通过搜索引擎找到答案. ----不记得谁说过了网络本来就是程序员们构建的, 所以在网络上跟程序相关的资源非常非常多, 比眼科图谱多多了. 两个主要的搜索工具:

Google: 这是通用的搜索引擎, 一般用python或者numpy+你需要的关键词, 比如random, 用google搜索到的往往是相关的文档
Stackoverflow: 这是更加面向程序员的社区, 里面更多是面向具体问题的解决方案, 很多已经给出了代码, 复制粘贴过来重新理解一下, 也许就可以用了.

搜索本身就是学习过程, 不要指望你在什么都不知道的情况下就能直接搜索到需要的内容. 更多情况下是一边搜索, 一边学习, 逐渐缩小自己使用的关键词. 在搜索过程中, python的中文内容也是不少的, 不过, 我更推荐你以此练练英语, 有很多词汇中文翻译得反而更难理解. 还不如直接看英文呢.

关于np.random我就不详细解释了, 这只是为了后面使用多人数据随机产生的一组数据而已, 更常见的多人数据, 很可能是来自于一个excel文件, 不过请先按下好奇心, 我们先从基本的开始.

计算单个IOL的SRK2公式¶

把我们之前写过的SRK2公式拿出来看看:

def SRK_2_origin(A,K_1,K_2,L,REF=0):
    if L < 20.0 :
        A1=A+3
    elif L < 21.0 :
        A1=A+2
    elif L < 22.0 :
        A1=A+1
    elif L == 22.0:
        A1=A
    elif L > 22.0 and L < 24.5 :
        A1=A
    elif L >= 24.5:
        A1=A-0.5
    
    K = (K_1+K_2)/2
    P_emme= A1- 0.9*K -2.5*L
    
    if P_emme < 14:
        CR = 1.00
    else:
        CR = 1.25
        
    P_ammc=P_emme-REF*CR
    return P_ammc

把前面产生的数据代入, 计算一下SRK2公式算出的结果.

print(SRK_2_origin(A,K_1,K_2,L,REF))

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-3-49cd03eadbeb> in <module>()
----> 1 print(SRK_2_origin(A,K_1,K_2,L,REF))

<ipython-input-2-c9621155cb1a> in SRK_2_origin(A, K_1, K_2, L, REF)
      1 def SRK_2_origin(A,K_1,K_2,L,REF=0):
----> 2     if L < 20.0 :
      3         A1=A+3
      4     elif L < 21.0 :
      5         A1=A+2

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

看到出错了吧, 很多时候在编写面向大量数据的函数时, 处理和面向单独一个数的会有差别. 如果没考虑到这样的差别就会出错了.

这里面的错误主要是发生在SRK2公式要根据眼轴长L来修正A常数的过程.

因为我们传给SRK_2_origin函数的L, 里面包含有5个数, 而不是1个数, 处理的时候要同时处理5个数, 而不仅仅是一个. 这就是所谓的

向量¶

patient_number=5
L=np.random.rand(5,1)*4+23

print(L)
print("L的类型: ")
print(type(L))

[[ 25.88253062]
 [ 25.32807917]
 [ 25.14949292]
 [ 26.0344625 ]
 [ 23.42363043]]
L的类型: 
<class 'numpy.ndarray'>

L=np.random.rand(5,1)*4+23

产生了5行1列的一个类型为'numpy.ndarray'的列向量. 其中(5,1)是描述向量的形态shape的.

print(L.shape)

(5, 1)

还可以有很多产生ndarray的方法, 不仅仅是列向量, 也可以产生二维的矩阵, 比如:

x=np.arange(12).reshape(3,4)
print(x)
print(x.shape)

[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
(3, 4)

np.arange(N)是产生0到N-1的N个数, reshape是把一个向量或者矩阵转变形状, 这里就是把0-11这12个数字, 排列乘3行4列的二维矩阵.

还需要提示一个小技巧, numpy在处理单独一行或者单独一列的向量时, 会把1省去, 不要这样写, 最好用reshape把1行或者1列的形态标记清楚.

U=np.arange(3)
print('U={0}, \tU.shape={1}'.format(U, U.shape)) #此处打印展示了诸多奇技淫巧, 如有兴趣可自行搜索
V=np.arange(3).reshape(-1,1) # 这里的-1表示什么猜猜看
print('V={0}, \n\t\tV.shape={1}'.format(V, V.shape))

U=[0 1 2], 	U.shape=(3,)
V=[[0]
 [1]
 [2]], 
		V.shape=(3, 1)

矩阵内容的提取¶

我们可以单独提取出矩阵中的一部分, 比如, 第0行, 注意python的计数是从0开始的, 务必小心这一点:

x=np.arange(12).reshape(3,4)
print(x[0, : ])

[0 1 2 3]

这里使用方括号[ ] 来示意是要索引, [0,:]中的冒号: 是说所有的部分. 也可以提取出矩阵中的一小部分, 比如:

print( x[0:3, 1:2])

[[1]
 [5]
 [9]]

冒号的右侧, 表示<, 而不是<=, 所以1:2, 和1是一回事. 还可以按照一定的逻辑判断来提取, 比如:

print( x[x>4])

[ 5  6  7  8  9 10 11]

这个特点就是我们在后面需要使用的了. 比如对于SRK2公式, L > 22.0 and L < 24.5 时, A常数不变. 我们可以使用一个特殊的np.logical_and() 来处理对矩阵的逻辑运算.

pickout=np.logical_and(L>22, L<24.5)
print(pickout)
print( A[pickout] )

[[False]
 [False]
 [False]
 [False]
 [ True]]
[ 118.]

计算多个IOL的SRK2公式¶

要使SRK2公式能够面向多个数计算, 也就是能够对向量计算, 就要改造一下之前的if语句. 比如之前:

if L < 20.0 :
    A1=A+3

已经不适合对L向量和A向量进行处理了. 我们可以改造成:

A[L<20.0] = A[L<20.0] + 3
print(A)

[[ 118. ]
 [ 118.4]
 [ 119. ]
 [ 119. ]
 [ 118. ]]

类似的, 可以构造一个根据L修正A常数的函数:

def on_L_change_A(L,A,Lmin,Lmax,deltaA):
    pickout=np.logical_and(L>Lmin, L<=Lmax)
    A[pickout] += deltaA
    return A

有了这个函数, 再去定义SRK2公式的函数, 就可以躲开出错的if语句了.

练习¶

利用on_L_change_A函数修改新的SRK_2公式函数, 使之可以满足同时处理多组数据.

第一处¶

使用on_L_change_A函数, 替代if. . . elif. . . 语句, 例如

if L < 20.0 :
    A1=A+3

修改成了

A = on_L_change_A(L,A,0,    20,    3) # 我想眼轴长L应该不至于<0, 因此用0作为下界

if L > 24.5 :
    A1=A-0.5

修改成了

A = on_L_change_A(L,A,24.5, 50,    -0.5) # 我想眼轴长L应该不至于 > 50, 因此用50作为上届

补充下面关于A的修正过程, 将含有None修改成合适的语句.

第二处¶

if P_emme < 14:
        CR = 1.00
    else:
        CR = 1.25

已经首先使用

CR = np.ones(P_emme.shape)

将CR的默认值设定成了元素为1, 形状与P_emme相同的矩阵, 请将 P_emme >=14 时所对应的CR值, 修改成 = 1.25

你可能需要在CR[?]里面增加一些逻辑判断.

def SRK_2(A,K_1,K_2,L,REF=0):
    A = on_L_change_A(L,A,0,    20,    3)
    # 在此行下面修改代码, 不要改变此行之前的代码
    A = None
    A = None
    A = None
    # 在此行上面修改代码, 不要改变此行之后的代码
    A = on_L_change_A(L,A,24.5, 50,    -0.5)

    K = (K_1+K_2)/2
    P_emme= A - 0.9*K -2.5*L
    CR = np.ones(P_emme.shape)
    # 在此行下面修改代码, 不要改变此行之前的代码
    # CR[ ? ]=1.25
    # 在此行上面修改代码, 不要改变此行之后的代码
        
    P_ammc=P_emme-REF*CR # 注意这里的乘法
    return P_ammc

print(SRK_2(A,K_1,K_2,L,REF))

期望的答案是:

[[ 15.04981622]
 [ 17.25996816]
 [ 21.6124319 ]
 [ 19.0135103 ]
 [ 26.33189411]]

处理5个病人的数据, 和处理一千零一个人的数据并没有区别.