Scikit-learn笔记2
Applied Machine Learning in Python
这门课实在是太差了. 严重差评:
- 本身讲得就很差, 还经常口误
- 不写板书, 对着ppt念
- 代码写得也混乱, 在函数内部用import? ?
- 交作业的时候要手动注释掉matplotlib
- 考试填空题是给出函数的运行结果
我上大学时上毛泽东思想概论和邓小平理论的课听着都比这舒坦.
作为报复, 我决定把第三周的ppt给丫翻译了!
评估¶
- 不同的应用可能有非常不同的目标
- Accuracy虽然广泛使用, 但其他的评估指标也可能使用. 例如:
- 用户满意度 (网络搜索)
- 收入(电子贸易)
- 病人生存率的提高(医疗)
不平衡分类中的Accuracy¶
- 假设有两个分类:
- 相关(R): 阳性分类结果
- 不相关(N): 阴性分类结果
- 随机选择1000个样本, 平均而言: Out of 1000 randomly selected items, on average
- 1个R
- 999个N
你建了一个分类器, 在test set上测试后发现accuracy=99.9%
- Wow! Amazingly good! 是不是?
- 为了比较, 假定我们有一个"dummy"分类器, 就是个假分类器, 不管输入是什么, 都预测是最多频率的类别, 比如N
那么 $$ Accuracy_{DUMMY} = \frac{999}{1000}=99.9\% $$
Dummy分类器完全忽略输入数据¶
- scikit-learn中常用的DummyClassifier类型:
- most_frequent: 预测值是出现频率最高的类别
- stratified : 根据训练集中的频率分布给出随机预测
- uniform: 使用等可能概率给出随机预测
- constant: 根据用户的要求, 给出常数预测.
- 这个方法的主要动机是F1-scoring, 当阳性分类很少的情况.
如果你的模型预测结果跟Dummy差不多:
- 功能无效,错误或缺失
- 内核或超参数选择不当
- 分类失衡, 有的类别太多
重点重点: Binary prediction outcomes¶
| 预测为(-) | 预测为(+) | |
|---|---|---|
| 实际为(-) | TN | FP |
| 实际为(+) | FN | TP |
- TP = true positive 真阳性
- FP = false positive (Type I error) 假阳性(Type I错误) , 印象里就是P<0.05的0.05
- TN = true negative 真阴性
- FN = false negative (Type II error)假阴性(Type II错误)
上面的矩阵叫做: Confusion-Matrix
-
Accuracy: 分类正确的概率. 实际为(-)预测为(-), 实际为(+)预测为(+)叫做正确. $$ Accuracy=\frac{TP + TN}{TP + TN + FP + FN} $$
-
Classification error: (1-Accuracy), 分类错误的概率 $$ Classification\; error=\frac{FP + FN}{TP + TN + FP + FN} $$
-
Recall, 真阳性率: 实际上为(+), 能够被预测成(+)的概率
- Recall又叫
- True Positive Rate (TPR): 真阳性率
- Sensitivity: 敏感性
- Probability of detection: 检出率 $$ Recall=\frac{TP}{TP+FN} $$
-
Precision: 如果预测为(+), 那么预测正确的概率 $$ Precision=\frac{TP}{TP+FP} $$
-
False positive rate (FPR): 假阳性率, 误报率. 本来实际上是(-)的, 结果分类器报告成(+)的概率
- 又叫做: Specificity, 特异性 $$ False positive rate=\frac{FP}{TN+FP} $$
precision与recall的折衷¶
-
Recall指导的机器学习任务:
- 法律搜索和法律信息提取
- 肿瘤检测Tumor detection
- 通常配备人类专家剔除假阳性
-
Precision指导的机器学习任务
- 搜索引擎排序, 搜索建议
- 文档分类
- 很多面向用户的任务(因为用户记住错误!)
F1-score: 结合precision与recall¶
$$ F_1=2\frac{precision \times recall}{precision+recall}=\frac{2TP}{2TP+FN+FP} $$F-score: 更一般地将precision与recall结合成单独一个数¶
$$ F_\beta=(1+\beta^2)\frac{precision \times recall}{\beta^2\times precision+recall}=\frac{(1+\beta^2)TP}{(1+\beta^2)TP+FN+FP} $$𝛽用来调整recall vs precision之间的重要程度:
- Precision-oriented users: 𝜷 = 0.5
- Recall-oriented users: 𝜷 = 2
In [6]:
def compute_scores(TP,TN,FP,FN):
# Accuracy = TP + TN / (TP + TN + FP + FN)
# Precision = TP / (TP + FP)
# Recall = TP / (TP + FN) Also known as sensitivity, or True Positive Rate
# F1 = 2 * Precision * Recall / (Precision + Recall)
scores_dict={}
scores_dict["Accuracy"] = (TP + TN) / (TP + TN + FP + FN)
scores_dict["Precision"] = TP / (TP + FP)
scores_dict["Recall"] = TP / (TP + FN) # Also known as sensitivity, or True Positive Rate
scores_dict["F1"] = 2 * scores_dict["Precision"] * scores_dict["Recall"] / (scores_dict["Precision"] + scores_dict["Recall"])
return scores_dict
In [5]:
c_matrix={"TN":19,"FP":8,
"FN":4, "TP":96}
compute_scores(96,19,8,4)
Out[5]:
未完待续¶
In [ ]:
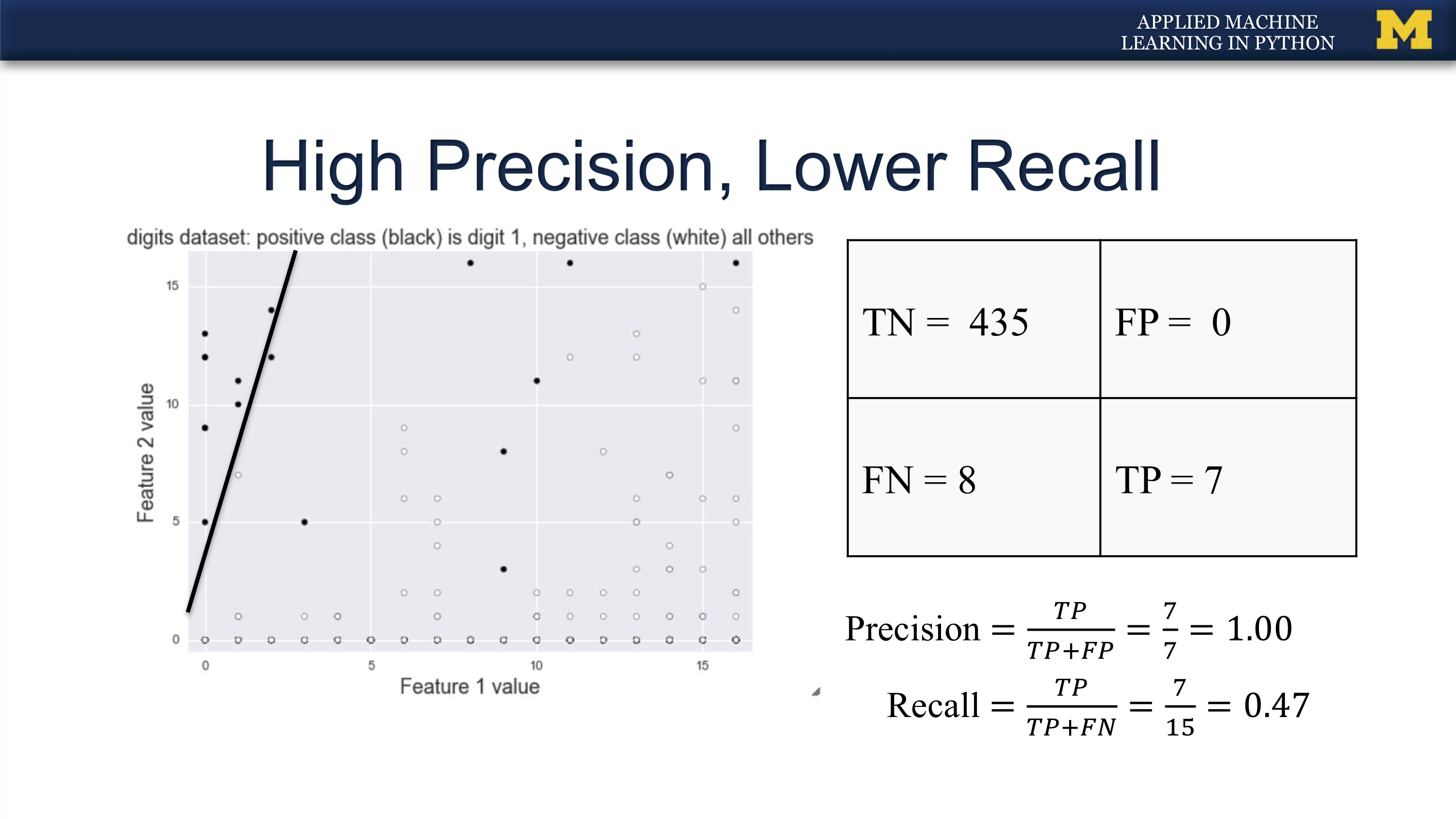 无罪推定, 抓到的坏人都是有罪的, 但也可能有很多漏网了.
无罪推定, 抓到的坏人都是有罪的, 但也可能有很多漏网了.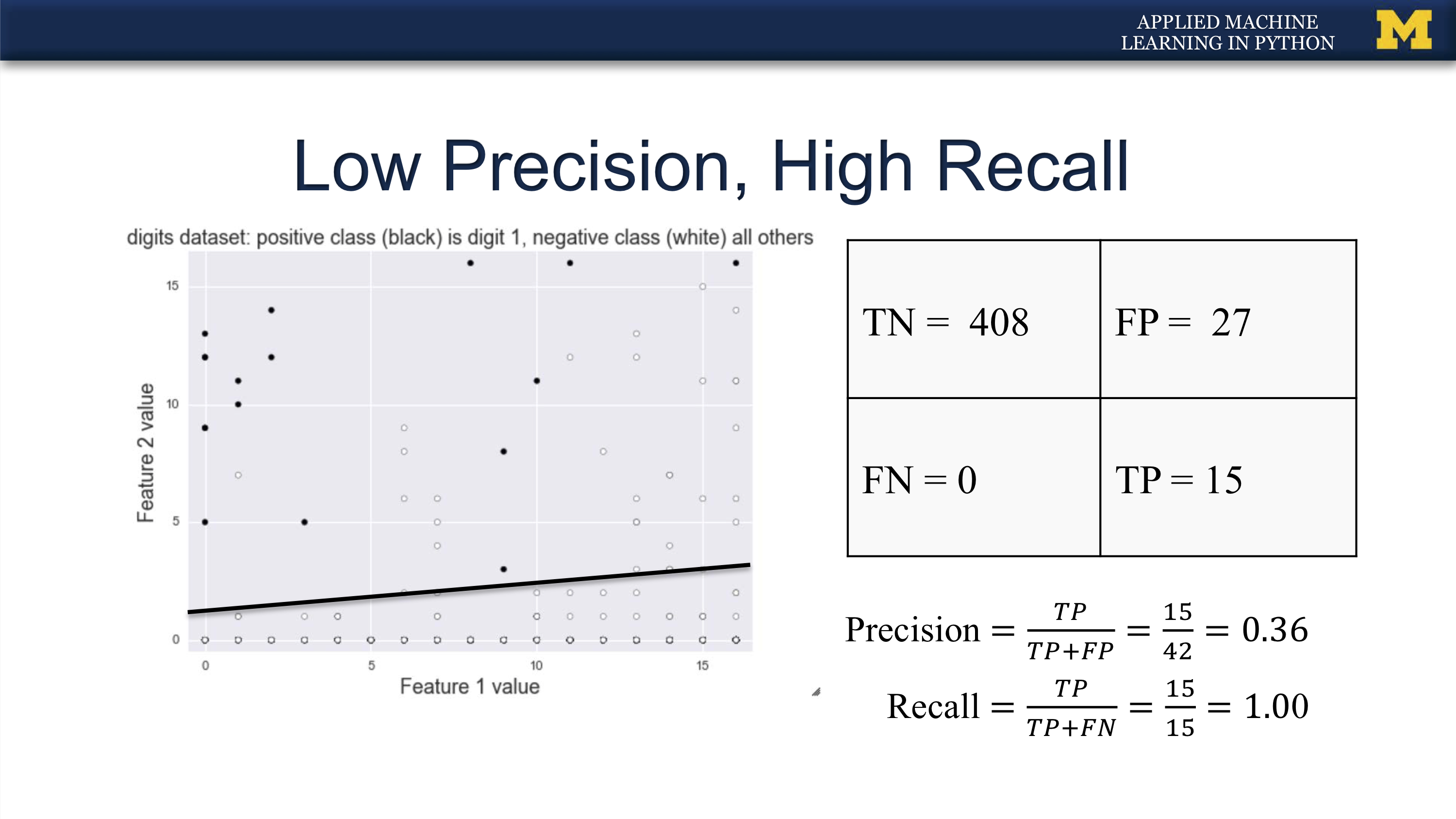 宁肯错杀一千, 不可放走一个.
宁肯错杀一千, 不可放走一个.