Pancake光路

源文件

Facebook发了一篇非常华丽的paper, 里面用全息(Holographic, 原教旨意义的全息, 不是各种市场部吹嘘的引申假借)做了一个超薄的VR眼镜.

Holographic-optics

完全是一副未来已来的样子.

不过我在看文献的时候, 却对里面回顾的另一个光路很感兴趣.

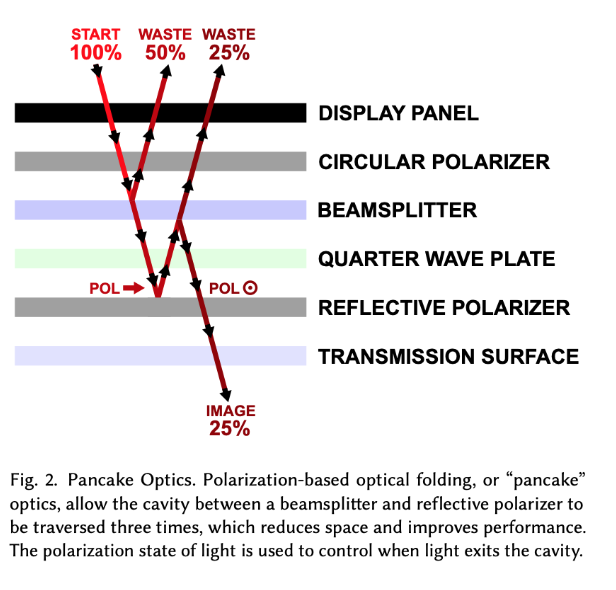
这个光路令光线往返了3次, 可以将光程缩短为原来的1/3, 当然也是有代价的, 代价是亮度降低到原来的25%, 不过看起来很有趣, 而且是一种通用的方案, 在其他的光路设计上也很有可能使用到. 同时, 对于其中元件的微小移动都可能造成3倍的光程变化, 对于调焦可能也很有用.

于是我就决定用Jones矢量和Jones矩阵推导一下, 看看光路中到底发生了什么.

Jones矢量与Jones矩阵

以下使用sympy进行符号运算

In [14]:
from sympy import *

Jones矢量

定义常见的Jones矢量,

参考定义一定要说清楚, 不然不同书里不一样, 特麻烦, 本文的参考定义来自:

In [15]:
def jones_vector(dictname):
    vector={
        'linear polarized light' : Matrix([1,0]),
        'θ linear polarized light': Matrix([cos(θ), sin(θ)]),
        'right-hand circularly polarized light': Matrix([1/sqrt(2), -I/sqrt(2)]), # (2.35)
        'left-hand circularly polarized light': Matrix([1/sqrt(2), +I/sqrt(2)]), # (2.36)
    } 
    return vector[dictname]

例如,

  • 光矢量沿x轴的线偏振光
  • 光矢量与x轴π/4的线偏振光
  • 右旋圆偏振光
In [16]:
θ=symbols('θ')
print('光矢量沿x轴的线偏振光:')
pprint(jones_vector('linear polarized light'))
print()

print('光矢量与x轴π/4的线偏振光:')
pprint(jones_vector('θ linear polarized light').subs(θ, pi/4))
print()

print('右旋圆偏振光:')
pprint(jones_vector('right-hand circularly polarized light'))
print()

光矢量沿x轴的线偏振光:
⎡1⎤
⎢ ⎥
⎣0⎦

光矢量与x轴π/4的线偏振光:
⎡√2⎤
⎢──⎥
⎢2 ⎥
⎢  ⎥
⎢√2⎥
⎢──⎥
⎣2 ⎦

右旋圆偏振光:
⎡  √2  ⎤
⎢  ──  ⎥
⎢  2   ⎥
⎢      ⎥
⎢-√2⋅ⅈ ⎥
⎢──────⎥
⎣  2   ⎦

Jones矩阵

定义常见偏振器件的Jones矩阵,

参考定义来自:

其中快轴(或透光轴)位于x轴方向. 采用线性Retarder对快轴保持不变的形式. 此处用力吐槽一下, 如前所见, 偏振光用二元向量描述快轴和慢轴, 偏振元件也就是改变这两的属性, 对于旋转的, 类似于调时钟的时针和分针, 也许目的只是让两者之间张开90度, 那么:

  • 可以保持快轴不变, 转慢轴,
  • 也可以保持慢轴不变转快轴,
  • 还可以中间选个平均位置不变, 一边转快轴, 一边转慢轴

这三种都可以, 得到的转换矩阵形式上是不同的, 当然互相之间可以再转换. 但是一本书一定要写清楚, 而且要保持一致才好, 否则在看例题的时候就可能陷入混乱. 我开始看一本中文书、一本英文书, 都没说自己用了哪种定义, 中文书里还前后标准不一致, 害得我查了半天程序, 又查第三本书.

In [17]:
def basic_jones(dictname):
    ϕ , δ=symbols('ϕ δ')
    # Table 5.3 Polarizer Jones Matrices
    jones_dict={
#         Polarizer Jones Matrices
        'polarizer' : [1,0,0,0], 
        'right circular polarizer': [1/2 * 1, 1/2 * I, 1/2 * (-I), 1/2 * 1],
        'left circular polarizer' : [1/2 * 1, 1/2 * (-I), 1/2 * (I), 1/2 * 1],
        
#         Linear Retarder Jones Matrices
#         Fast axis unchanged convention, 
#         delays the phase of the slow eigenpolarization, 
#         leaving the fast eigenpolarization’s phase unchanged
        'linear retarder': [1,0,0,exp(I*δ)],
        'quarter wave plate': [1,0,0,I],
        'right circular QWRCR': [1/2* (1+I), 1/2* (1+I), 1/2* (-1-I), 1/2* (1+I) ],
        'left circular QWLCR': [1/2* (1+I), 1/2* (-1-I), 1/2* (1+I), 1/2* (1+I)],
        
        'half wave plate': [1,0,0,-1],
        'right circular CR': [0,I,-I,0],
        'left circular LR': [0,-I,I,0],
        
#         查不到反射镜的Jones矩阵
#         反射过程似乎不这么简单, 但如果是垂直入射, 类比于声波可能就原路返回,
        'mirror': [-1,0,0,-1], 
        
    }
    a,b,c,d=jones_dict[dictname]
    return Matrix([[a,b],[c,d]])

当快轴与x轴有一定角度时, 使用旋转坐标系的方式计算出具有角度的偏振器件Jones矩阵.

In [18]:
def rotate_jones(dictname, x=0):
    R=Matrix([[cos(x), -sin(x)],[sin(x),cos(x)]])
    R_inv=Matrix([[cos(x), sin(x)],[-sin(x),cos(x)]])
    return R*basic_jones(dictname)*R_inv

例如:

  • 水平线性偏振器
  • 垂直线性偏振器
  • 135度线性偏振器
  • 45度1/4波片
  • 135度半波片
In [19]:
θ, ϕ = symbols('θ ϕ')
print('Horizontal linear polarizer HLP, L(0°):')
pprint(rotate_jones('polarizer'))
print()

print('Vertical linear polarizer VLP:')
pprint(rotate_jones('polarizer' ,pi/2))
print()

print('135° Linear polarizer L(135°):')
pprint(rotate_jones('polarizer' ,pi/4*3))
print()

print('45° Quarter Wave LR (π/2, 45°)')
pprint(rotate_jones('quarter wave plate', pi/4))
print()

print('135° Half Wave LR (π, 135°)')
pprint(rotate_jones('half wave plate', pi/4*3))
print()

Horizontal linear polarizer HLP, L(0°):
⎡1  0⎤
⎢    ⎥
⎣0  0⎦

Vertical linear polarizer VLP:
⎡0  0⎤
⎢    ⎥
⎣0  1⎦

135° Linear polarizer L(135°):
⎡1/2   -1/2⎤
⎢          ⎥
⎣-1/2  1/2 ⎦

45° Quarter Wave LR (π/2, 45°)
⎡1   ⅈ  1   ⅈ⎤
⎢─ + ─  ─ - ─⎥
⎢2   2  2   2⎥
⎢            ⎥
⎢1   ⅈ  1   ⅈ⎥
⎢─ - ─  ─ + ─⎥
⎣2   2  2   2⎦

135° Half Wave LR (π, 135°)
⎡0   -1⎤
⎢      ⎥
⎣-1  0 ⎦

Pancake 光路

不失一般性, 设Display Panel发出水平线性偏振光.

In [20]:
light=jones_vector('linear polarized light')
pprint(light)

⎡1⎤
⎢ ⎥
⎣0⎦

第一次光程

分别穿过如下光学器件:

  • right circular polarizer
  • beam splitter, 假设偏振性不变
  • quarter wave plate

到达reflective polarizer

穿过right circular polarizer

由水平线性偏振光变成了右旋圆偏振光

In [21]:
light=rotate_jones('right circular polarizer') * light
pprint(light)

⎡ 0.5  ⎤
⎢      ⎥
⎣-0.5⋅ⅈ⎦

穿过beam splitter,

假设偏振性不变, 仍然是右旋圆偏振光

穿过quarter wave plate

从右旋圆偏振光变成与x轴45度的线性偏振光

In [22]:
light=rotate_jones('quarter wave plate') * light
pprint(light)

⎡0.5⎤
⎢   ⎥
⎣0.5⎦

到达reflective polarizer

视reflective polarizer为polarizer与镜面的结合, 如果reflective polarizer发生反射, 说明reflective polarizer与光线的偏振方向垂直, 所以reflective polarizer应该是135度的线性偏振器, 两者垂直, 那么光线应该无法穿过该偏振器, 也就是乘出来为0向量

In [23]:
reflective_polarizer = rotate_jones('polarizer', pi/4*3)
pprint(reflective_polarizer * light )

⎡0⎤
⎢ ⎥
⎣0⎦

第二次光程

  • 经过reflective polarizer的反射, 不妨假定是垂直入射的镜面反射
  • 通过quarter wave plate

到达beam splitter

在reflective polarizer上反射

从x轴45度的线性偏振光仍然变成线性偏振光, 按说方向是相反的, 但我也不知道正确的镜面Jones矩阵应该怎么写, 姑且认为是线性偏振光原路返回

In [24]:
light = rotate_jones('mirror')*light
pprint(light)

⎡-0.5⎤
⎢    ⎥
⎣-0.5⎦

第二次通过quarter wave plate

从线性偏振光变成了左旋圆偏振光

In [25]:
light=rotate_jones('quarter wave plate') * light
pprint(light)

⎡ -0.5 ⎤
⎢      ⎥
⎣-0.5⋅ⅈ⎦

第三次光程

  • 经过beam splitter的反射, 不妨假定是垂直入射的镜面反射
  • 经过quarter wave plate

到达reflective polarizer

在beam splitter上反射

继续是左旋圆偏振光, 注意, 这时候与第一次光程时的旋转方向相反了

In [26]:
light = rotate_jones('mirror')*light
pprint(light)

⎡ 0.5 ⎤
⎢     ⎥
⎣0.5⋅ⅈ⎦

第三次通过quarter wave plate

从左旋圆偏振光变成了135度线性偏振光

In [27]:
light=rotate_jones('quarter wave plate') * light
pprint(light)

⎡0.5 ⎤
⎢    ⎥
⎣-0.5⎦

抵达reflective polarizer

验证一下此时能否穿过reflective polarizer, 如果可以通过, 应该跟之前一致

In [28]:
pprint(reflective_polarizer * light )

⎡0.5 ⎤
⎢    ⎥
⎣-0.5⎦

Q.E.D

PS.

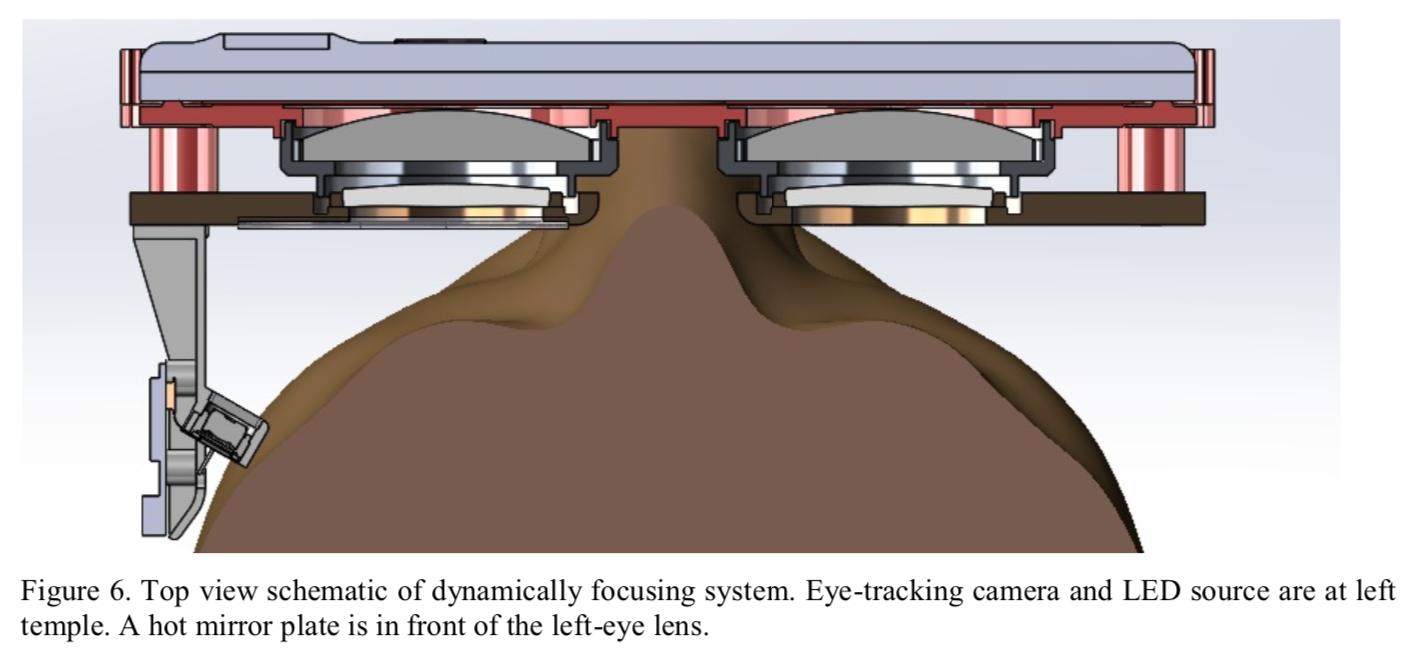
Pancake光路也做出了很轻薄的头戴显示器, 发文章的居然是3M, 在这篇文章中, 他们使用步进电机移动beamsplitter, 造出了变焦版本的头戴显示器, 通过追踪瞳孔位置估算出人眼对焦位置, 然后再变焦, 由于3倍折叠光路以后所需要移动的位置很小, 所以响应可能更好.

3M fig6

In [ ]: