SARI数据分析(1): 控制新出现流行病的非药物干预措施比较
控制新出现流行病的非药物干预措施比较
Comparing nonpharmaceutical interventions for containing emerging epidemics
2017年, 发在PNAS, 作者是哈佛大学公共卫生学院和哈佛医学院, 目前被引用13次, 全文: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5393248/
以下先读懂原文, 然后再看看能否根据原文的模型, 拟合一个SARI的模型出来. (点击右上的“源文件”, 可以下载本文自行运行其中代码)
方法¶
定义:¶
- “接触者追踪”(Contact tracing)是识别和评估接触过某种疾病的人的过程。 有症状的接触者被立即隔离; 没有症状的接触者被隔离或者接受症状监测。
- “隔离”(Isolation)是分离一个有症状的被确认感染的个体。
- “检疫”(Quarantine) 是指被认为已暴露但目前未患病的个人的隔离(34)。 如果出现症状,他 / 她将被隔离并接受医疗护理。
- “症状监测”(Symptom monitoring)是对被认为暴露但没有生病的个人定期进行的症状评估。 如果发现症状,个人被隔离。
- “求医行为”(Health-seeking behavior)是指在出现症状时寻求医疗保健,导致隔离的行为。
感染后,产生传染性和出现症状前的天数分别为传染潜伏期 ($T_{LAT}$) 和症状潜伏期 ($T_{INC}$)
由于症状、病原体浓度和行为可在整个病程中变化,我们允许相对传染性(βτ)随时间 τ(自传染性发生以来)变化 。
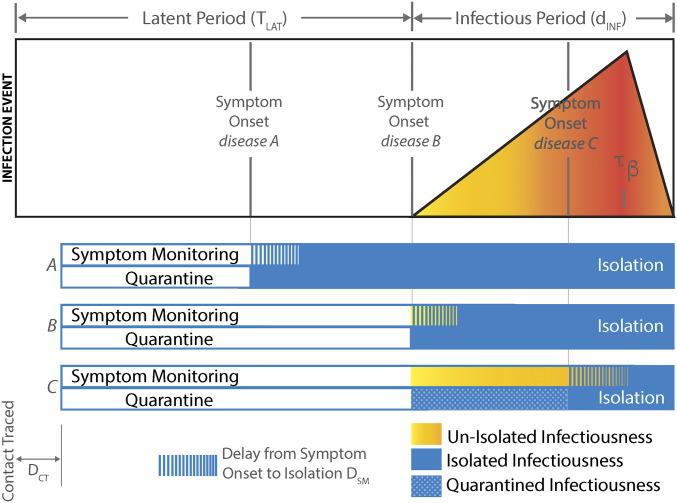
图1 (插图看似总是不成功, 如果图裂了, 就点击看原文的图吧)
图1: 疾病自然史和干预时机示意图。从感染事件的左侧开始,进展至传染潜伏期 ($T_{LAT}$),传染潜伏期内无传染性, 然后进入传染期 $d_{INF}$ 天,感染性晚期峰值 τβ。
对于 A–C 疾病,显示症状分别出现在传染性出现之前、同时出现和之后。我们在这里展示了一个个体,其在感染后不久被追踪,并在短暂延迟 $D_{CT}$ 后被置于症状监测或检疫之下。
- 最近的 SARS 和埃博拉流行病表明,医院隔离并不总是包含传播;因此,我们允许隔离有效性 (γ) 发生变化,以反映不同的环境。
- 被追踪 ($P_{CT}$) 的接触者比例可以小于 1,包括未能回忆接触者的有症状感染者、无症状的“沉默”感染事件和识别接触者的挑战。
- 风险分析中的缺陷和不确定性可减少真正感染的追踪接触者 ($P_{INF}$) 的比例。
- 追踪接触者的延误 ($D_{CT}$) 可能有许多原因,包括棘手的道路和人员限制。
- 症状发作和隔离之间的延迟 ($D_{SM}$) 特别适用于症状监测下的个体,并受监测频率、识别有时不可靠的临床特征的延迟和症状检测时及时隔离的延迟的影响。
干预参数:
| 参数名 | 变量 | 样例表现(最佳) | 样例表现(高) |
|---|---|---|---|
| 隔离效果 | γ | 1 | 0.9 |
| 追踪接触者的比例 | $P_{CT}$ | 1 | 0.9 |
| 被追踪接触者中真正感染的百分比 | $P_{INF}$ | 1 | 0.5 |
| 追踪接触者的延迟 | $D_{CT}$ | 0.25 ± 0.25 d | 0.5 ± 0.5 d |
| 从症状开始到隔离的延迟 | $D_{SM}$ | 0.25 ± 0.25 d | 0.5 ± 0.5 d |
| 从症状发作到求医行为的延迟 | $D_{HSB}$ | Disease-dependent | ∼unif(0, $d_{INF}$) |
模拟:¶
我们从疾病特异性输入分布中绘制每个模拟个体的疾病特征。
然后大概是说: 每小时的传染性τ, 定义为一个人新传染其他人的数量服从泊松分布, (如果是超级传播者, κ < 1, 就服从负二项分布) ,
该泊松分布的期望 = 个体产生的继续感染人数 (R0) x 相对传染性 βτ
(此处不是很理解, 请参考原文: with mean equal to the product of the expected number of onward infections for the individual (R0) and the relative infectiousness βτ )
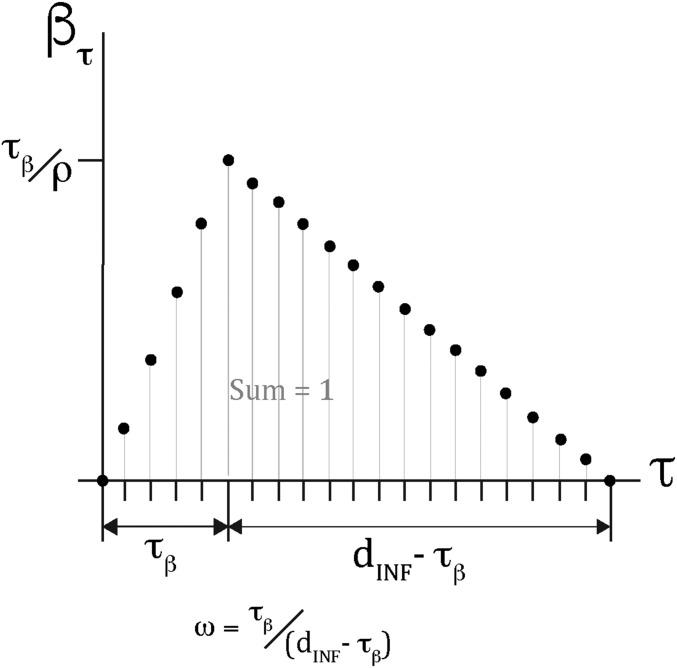
其中, $\sum_{\tau=1}^{d_{INF}} \beta_{\tau}=1$
假设随时间变化的的相对传染性遵循一个三角形分布,传染性峰值发生时间(τβ)可能在传染性开始到结束之间的任何时刻。
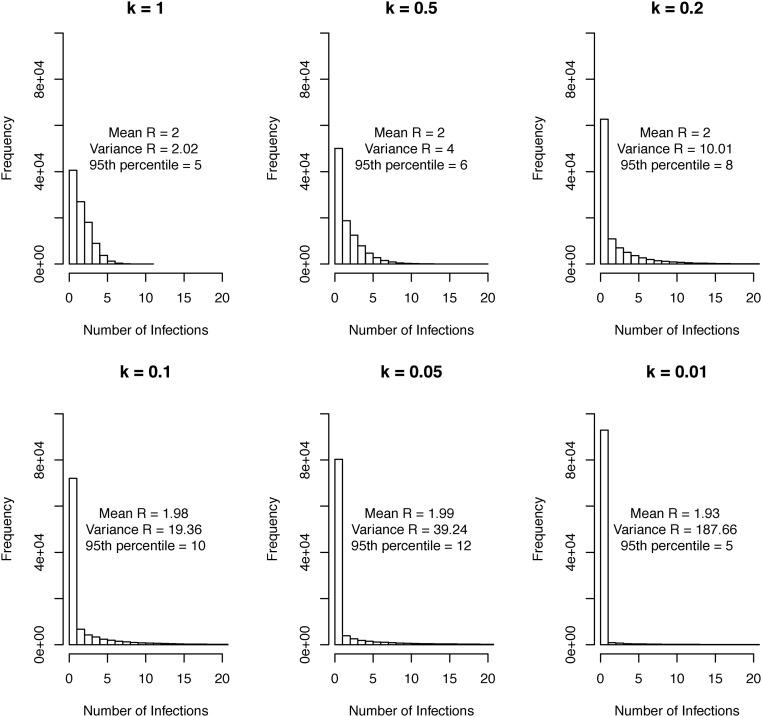
图S4 (请点击查看原文图片)
分散参数 (k) 的示意。在具有 100,000 个病原体的系统中,随着分散参数 (k) 的降低(即,产生更多的传播),每个感染个体产生的感染数量的方差增加,而均值近似恒定。
我们记录每个传播事件的传播日期和感染者,并为每个新感染者绘制疾病特征。 (下面几条还是在建模, 并不是真正知道这些数据)
- 在其感染者(感染这个新被感染者的人)被隔离的较早时间, 或在感染者被隔离时发生传染的较早时间,通过接触追踪概率 $P_{CT}$ 来识别个体。
- 在 $D_{CT}$ 日的操作滞后时间后,对接触者进行检疫、症状监测,或如果对已经出现症状的进行隔离。
- 被检疫或隔离的个体在其疾病的其余时间里, 传染性降低了 γ 因子。(因为被隔离了, 所以传染能力下降)
- 在症状出现后, 经过$D_{SM}$天, 个体被隔离。
参数化¶
与症状和疾病自然史相关的特征相比,传染性自然史的关键方面往往更难观察和测量。因此,我们采用序贯蒙特卡罗粒子滤波算法,
创建潜伏期与潜伏期的时间偏移 ($T_{OFFSET} = T_{LAT}−T_{INC}$)、传染性高峰时间 (τβ) 和传染性持续时间 (dINF) 的联合概率空间。
根据已发表观察结果限定的每个参数的无信息先验分布,我们模拟了 500 例初始个体的 5 代感染,并记录了模拟的连续间隔(即,在感染者-被感染者, 症状发作之间的时间)。(大概是A先出现症状时间是Ta, 然后A传染给B, B出现症状时间是Tb, 间隔时间=Tb-Ta)
对参数集进行重新采样,通过使用累积分布函数之间差异的 Kolmogorov–Smirnov 检验,模拟序列区间分布与已发表序列区间分布匹配程度确定重要性权重. (WTF, 关键步骤没看懂)
疾病参数:
| 来自公布估计数 | 来自公布估计数 | 来自公布估计数 | 通过顺序蒙特卡罗法拟合 | 通过顺序蒙特卡罗法拟合 | 通过顺序蒙特卡罗法拟合 | |
|---|---|---|---|---|---|---|
| 参数名 | 基本繁殖数 $R_0$ | 时序间隔 (d) | 潜伏期 $T_{INC}$ (d) | 潜伏期偏移$T_{OFFSET} = T_{LAT}−T_{INC}$ | 传染性最长持续时间$d_{INF}$(d) | 传染性高峰时间τβ(范围0-1) |
| 埃博拉 | ||||||
| 中位数(参考) | 1.83 (20) | 13.36 (20) | 7.87 (20) | 0.33 | 11.95 | 0.10 |
| [95% 置信区间] | [1.72, 1.94] | [2.66, 38.8] | [0.93, 28.2] | [0,* 1.01] | [10.0, 17.0] | [0, 0.37] |
| 甲型肝炎 | ||||||
| 中位数(参考) | 2.25† | 26.72 (21) | 29.11 (22) | −5.33 | 13.38 | 0.35 |
| [95% 置信区间] | [2, 2.5] | [20.7, 33.8] | [24.6, 34.1] | [−7.57, −3.26] | [3.16, 19.2] | [0, 0.98] |
| 甲型流感 | ||||||
| 中位数(参考) | 1.54 (23) | 2.20 (21) | 1.40 (24) | −0.23 | 2.99 | 0.49 |
| [95% 置信区间] | [1.28, 1.80] | [0.63, 3.76] | [0.63, 3.10] | [−0.76, 0.29] | [2.00, 4.87] | [0.02, 0.98] |
| MERS | ||||||
| 中位数(参考) | 0.95 (25) | 7.62 (26) | 5.20 (26) | −1.55 | 16.43 | 0.37 |
| [95% 置信区间] | [0.6, 1.3] | [2.48, 23.3] | [1.83, 14.7] | [−3.14, 0.02] | [9.59, 24.5] | [0.01, 0.96] |
| SARS | ||||||
| 中位数(参考) | 2.9 (29) | 8.32 (29) | 4.01 (24) | 0.16 | 21.60 | 0.10 |
| [95% 置信区间] | [2.2, 3.6] | [1.59, 19.2] | [1.25, 12.8] | [0,* 0.67] | [14.9, 26.8] | [0, 0.46] |
图S6(点击打开图片) 演示用SMC 参数化方法的 KS 距离. A 中的参数集生成的序列间隔(bar;蓝线)不能用参考序列间隔分布(绿线)来解释,KS 得分为 0.25。(B) SMC 算法生成的参数集的后续迭代,其中生成的串行间隔与参考串行间隔(相同的绿线)更一致。
(所以虽然方法没看懂, 但可能有现成的PySMC工具包可用https://predictivesciencelab.github.io/pysmc/ 我猜是某种贝叶斯参数估计的方法, 一会儿实在搞不定, 就先把MERS、SARS的参数先借来用用)
保持潜伏期分布恒定,我们拟合了潜伏期的偏移 ($T_{OFFSET}$),原因如下,包括与疾病表征 CDC 方法的一致性 这些时间的生物学预期均与病原体负荷相关,并简约地将每个特征限制为一个可解释的参数。对于传染性持续时间 (dINF),我们拟合了均匀分布的上限和下限 1 天。考虑到在此期间传染性的可变性,我们假设相对传染性 βτ 的三角形分布,并拟合了传染性峰值的时间 (τβ)。模型参数化的完整描述可以在 SI 文本中找到,通过 SMC 的参数化。
未完成草稿, 持续更新中