AI 4 Med 笔记(1.2)各种率

源文件

第一门课第二周, 主要讲

各种率

  • 真假阴阳各种率
  • 敏感性和特异性
  • 阳性预测率(PPV)和阴性预测率
  • 置信区间, ROC曲线, F1 score

我之前学Scikit-learn的时候, 笔记记得挺清楚的.

参考

而且这张图做得很好, 一张图说明问题, 先看图, 再看后面的计算方式:

例如有这样的结果:

预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120

以下表格中, 分子是红字, 分母是黄色背景, 考虑C的情况

Accuracy

  • 正确率
  • 有病没病都说对了的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ Accuracy=\frac{100+110+120}{100+6+11+1+110+12+2+7+120} $$

Recall

  • 敏感性, 检出率, 真阳性率.
  • 实际有病, 测出有病的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ Recall=\frac{120}{2+7+120} $$

Precision

  • 精确度, 阳性预测率, PPV
  • 测出有病, 还说对了的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ Precision=\frac{120}{11+12+120} $$

Specificity

  • 特异性, 真阴性率
  • 测出没病, 还说对了的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ Specificity=\frac{100+6+1+110}{100+6+1+110+2+7} $$

False Positive Rate

  • 假阳性率, 误报率
  • 本来没病, 测出有病的概率
预测=A 预测=B 预测=C
实际=A 100 6 11
实际=B 1 110 12
实际=C 2 7 120
$$ False Positive Rate=\frac{11+12}{100+6+11+1+110+12} $$

真假阴阳性

预测为(-) 预测为(+)
实际为(-) TN FP
实际为(+) FN TP
  • TP = true positive 真阳性
  • FP = false positive (Type I error) 假阳性(Type I错误) , 印象里就是P<0.05的0.05
  • TN = true negative 真阴性
  • FN = false negative (Type II error)假阴性(Type II错误)

敏感特异性

  • Accuracy: 分类正确的概率. 实际为(-)预测为(-), 实际为(+)预测为(+)叫做正确. $$ Accuracy=\frac{TP + TN}{TP + TN + FP + FN} $$

  • Classification error: (1-Accuracy), 分类错误的概率 $$ Classification\; error=\frac{FP + FN}{TP + TN + FP + FN} $$

  • Recall, 真阳性率: 实际上为(+), 能够被预测成(+)的概率

    • Recall又叫
    • True Positive Rate (TPR): 真阳性率
    • Sensitivity: 敏感性
    • Probability of detection: 检出率 $$ Recall=\frac{TP}{TP+FN} $$

  • Precision: 如果预测为(+), 那么预测正确的概率 $$ Precision=\frac{TP}{TP+FP} $$

  • False positive rate (FPR): 假阳性率, 误报率. 本来实际上是(-)的, 结果分类器报告成(+)的概率

$$ False Positive Rate=\frac{FP}{TN+FP} $$
  • Specificity, 特异性

应该是真阴性率(之前写错了), TNR, 实际上为(-), 能够被测成(-)的概率 $$ Specificity=\frac{TN}{TN+FN} $$

F1-score: 结合precision与recall

$$ F_1=2\frac{precision \times recall}{precision+recall}=\frac{2TP}{2TP+FN+FP} $$

F-score: 更一般地将precision与recall结合成单独一个数

$$ F_\beta=(1+\beta^2)\frac{precision \times recall}{\beta^2\times precision+recall}=\frac{(1+\beta^2)TP}{(1+\beta^2)TP+FN+FP} $$

𝛽用来调整recall vs precision之间的重要程度:

  • Precision-oriented users: 𝜷 = 0.5
  • Recall-oriented users: 𝜷 = 2

阳性预测率 PPV

实际上就是

  • Precision: 如果预测为(+), 那么预测正确的概率 $$ Precision=\frac{TP}{TP+FP} $$
$$ PPV = Precision = \frac{sensitivity \times prevalence}{sensitivity \times prevalence+(1 - specificity) \times (1 - prevalence)} $$

其中 prevalence=P(pos), 阳性结果的发生率. 如果自己都知道TP、FP的数据, 当然用简单的公式计算, 如果拿到的是一个标记好各种率的试剂盒, 或者是看一篇新闻报道, 对方把各种率搅合在一起, 那么可能就要通过后一种公式来计算

置信区间

比如某个概率p=0.80(95% CI 0.78, 0.82),

是说, 真实的概率p, 谁知道是啥, 有95%的概率, 会落在[0.78, 0.82]的范围内. 置信区间的范围和样本量有关, 样本量越大, 置信区间的宽度越窄.

ROC曲线

  • X轴: False Positive Rate 假阳性率
  • Y轴: True Positive Rate 真阳性率

左上顶点:

  • 理想点
  • False positive rate 假阳性率=0
  • True positive rate 真阳性率=1

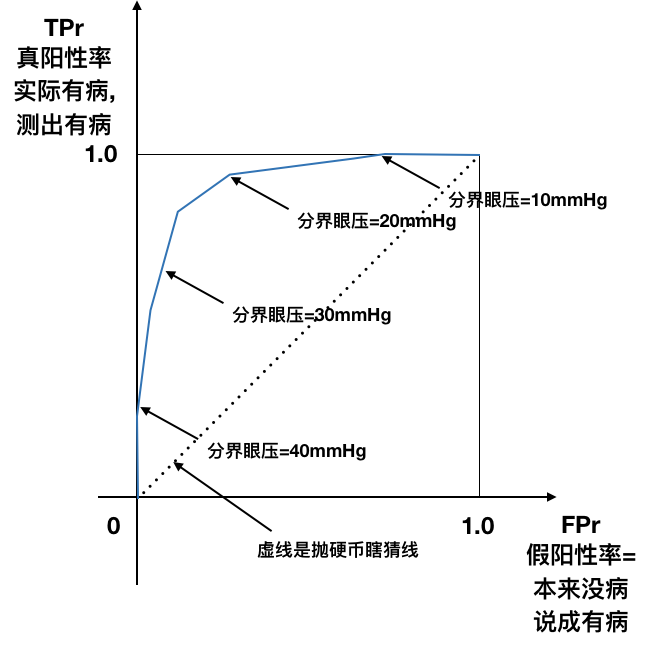
ROC.png

  • ROC曲线越往左上, 越好.
  • 曲线下面积(AUC), 越大越好
  • 45度线是随机瞎猜线

ROC-2.png