人工晶体度数计算公式推导(2)

考虑到Olsen T那篇综述后面基本是在吐槽, 没有继续讨论具体公式的推导. 所以我换一篇文献, 这次看的是Barrett Universal公式的初始形态, Intraocular lens calculation formulas for new intraocular lens implants80037-8)

1987年的Graham D. Barrett, M. D.还是一位具有分享精神并且自己会写GW Basic的青年. 不像现在这么吝啬, 满世界也翻不到他的Barrett Universal II和Barrett True K公式的解析形式, 只有网页上才有计算器.

眼科医生保有“公式的手算能力”是非常重要的, 谁知道哪个程序员会不会把毫米和米弄混, 把某个参数和另一个参数搞错? 真弄明白的时候都是大规模回顾数据的时候, 那时人工晶体早在眼内稳定好多年了.

大概那个乐于分享的时代快要逝去了吧.

Barrett Universal公式是基于Gaussian optical principals的, 是基于计算厚透镜用的公式, 于上集见到的薄透镜公式有所不同. 这里要考虑透镜的厚度, 还要考虑厚透镜的主平面

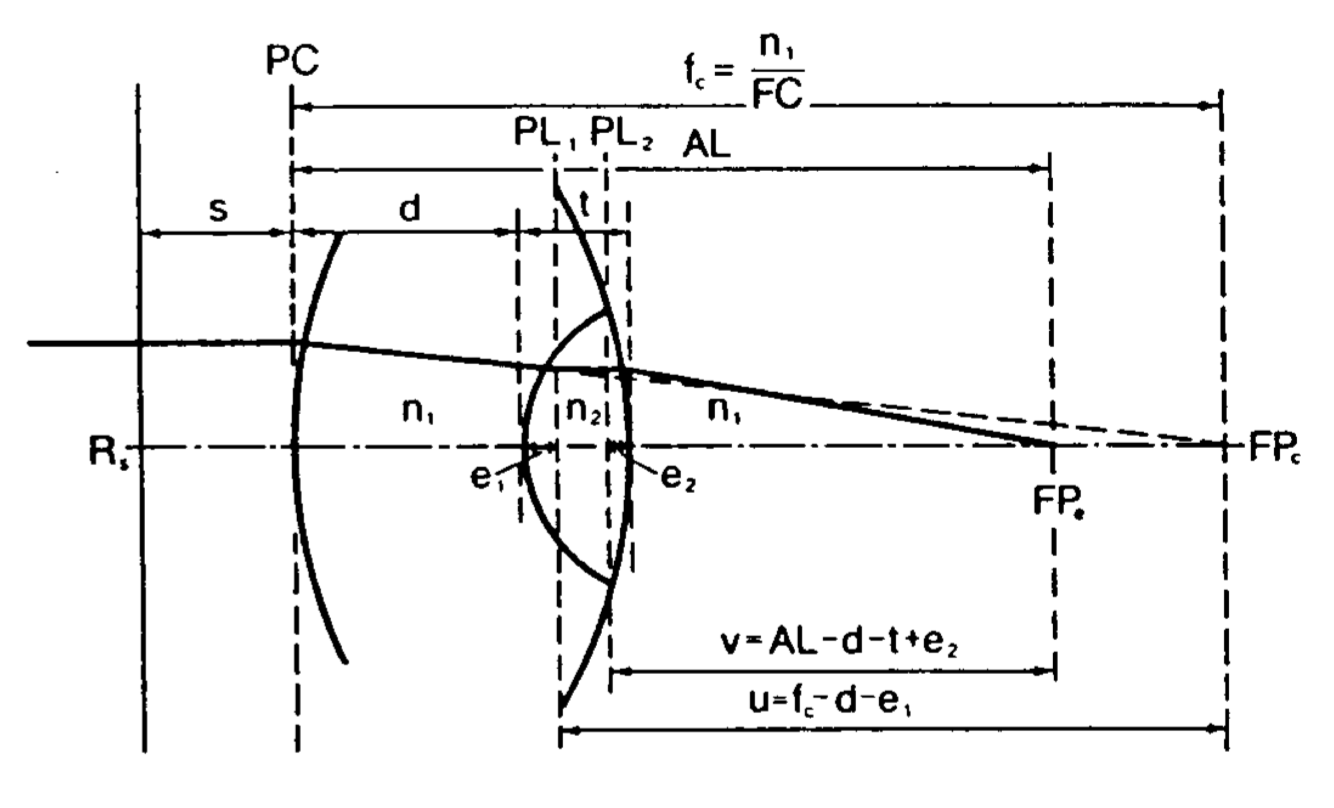
示意图看起来很复杂, 一点一点解释:

人工晶体就是中间的那个, Barrett当时是为了给水凝胶晶体推导公式, 所以人工晶体的长相比较奇怪. 设定人工晶体的厚度是t, 折射率是$n_2$, 人工晶体的前表面距离角膜顶点为d.

人工晶体前表面的屈光度是$FP_1$, 后表面的屈光度是$FP_2$, 接下来两个参数$e_1, e_2$要稍微解释下

回忆一下中学光学作图的时候, 画出一个薄透镜折射时, 我们只需要用一条直线代替透镜, 然后画出平行光与这个直线相交的点. 也就是把透镜当作一个没有厚度的平面来处理.

对于厚透镜, 要考虑前后两个面, 但这两个面的位置并不是紧贴着前后表面的顶点, 而是离开一点距离, 这两个面称为Principal Plane, 与光轴的交点成为Principal Point(主点).

Principal Plane, 是把入射光和出射光各自的延长线相交, 得到的平面. (补插图)

示意图中的$e_1, e_2$就是前后Principal Plane到透镜实际顶点之间的距离.

S是眼镜到角膜之间的距离, 眼镜度数Rs就是验光得到的结果, 角膜的屈光度是K