为什么对比敏感度的视标亮度是正弦变化的？(2)

现在让我们回到初中，回忆一下你已经还给物理老师的几何光学。

线性的几何光学

我们可以把透镜成像的过程当作是一个把“物”变换成“像”的功能，说实话function翻译成函数真是挡住了不少人，function嘛，其实就是功能而已，有输入，有输出，把输入变成输出的功能。

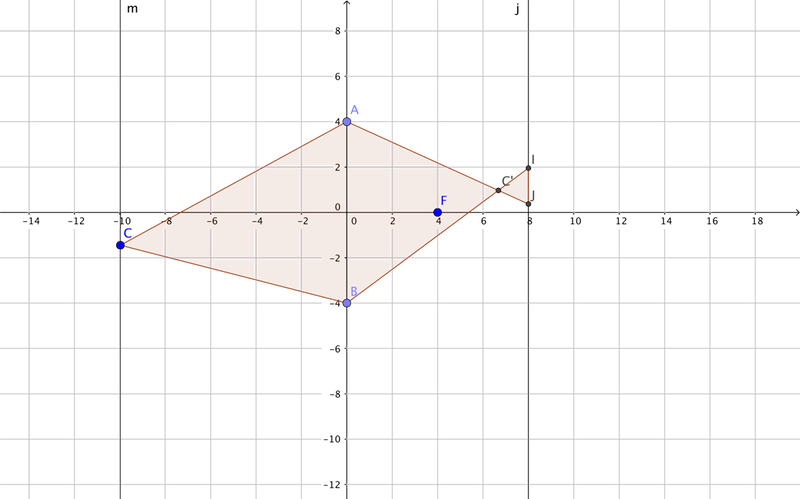输入一个物C，就可以在屏幕上得到一个光斑IJ。 f(点C)=IJ

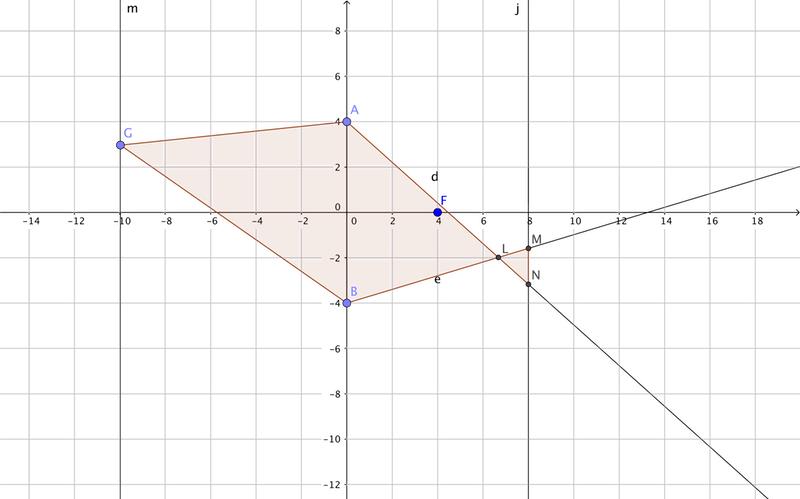输入另一个物G，就可以在屏幕上得到光斑MN。 f(点G)=MN

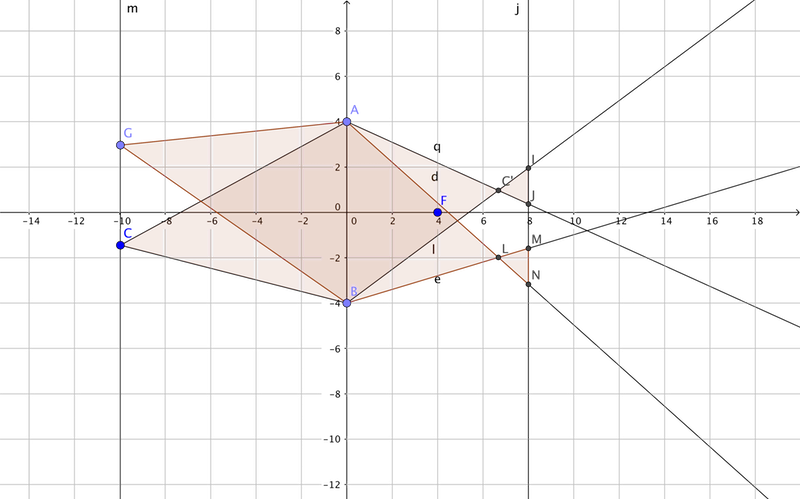
同时输入物C和物G，同时得到光斑IJ和光斑MN。 f(点C+点G)=IJ+MN = f(点C)+f(点G) 看，理想的成像过程是个线性系统。

线性不变系统

简单的说，就是这个系统的变换过程是不随时间改变或者不随空间改变的。

比如一个医生看一个结膜炎用3分钟，看2个结膜炎用6分钟。他早上8点开始就是这个速度，到12点快下班了，还是看一个结膜炎用3分钟，看2个结膜炎用6分钟。这就叫做线性时间不变。

对于成像来说，考虑的是空间。 比如离焦

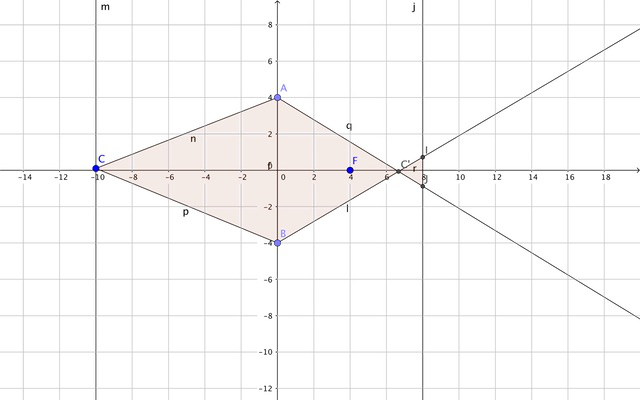
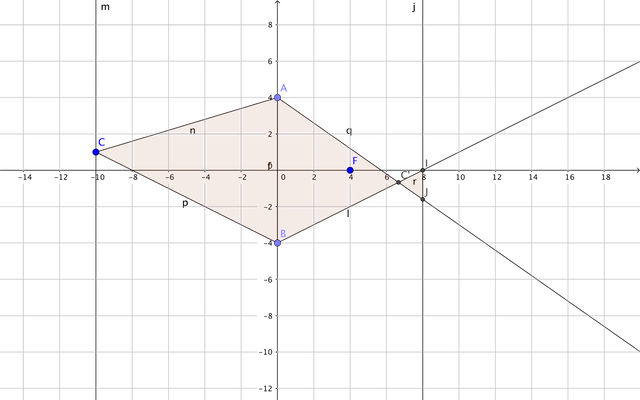
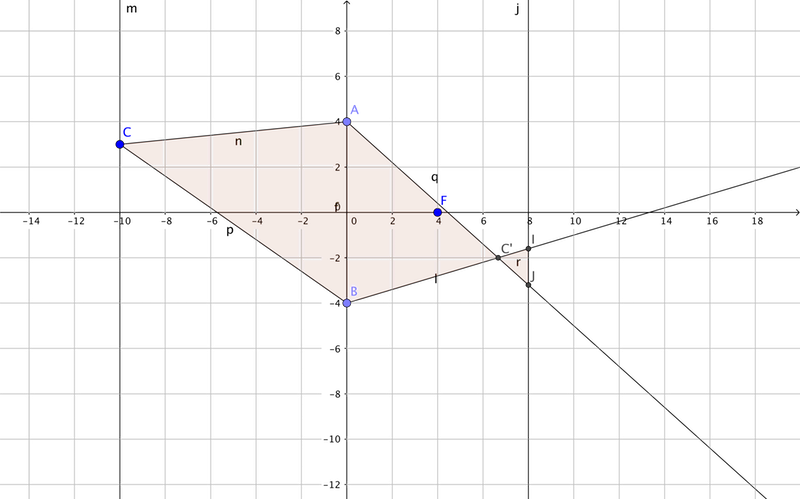
从C点发出光形成了光斑IJ，如果C点的位置在垂直于光轴的面上移动。那么光斑IJ的大小不变。

这很容易通过中学学习的几何光学证明，物距u，像距v，焦距f 1/u+ 1/v =1/f 物距u没变，所以像距v不变。 如果设光斑IJ的直径=x，屏幕到透镜的距离=L，透镜的直径=D 三角形ABC'与三角形JIC'相似。所以 IJ / AB = (L-V)/V 也就是 x / D = (L-V)/V x= D (L-V)/V 这里面D，L，V都是不变的，x当然也不变。

所以在垂直于光轴的同一个平面上移动物点C，得到的光斑IJ，虽然位置不同，但大小总是一样的。甚至，如果我们特别仔细地把光束分成一份一份，会发现光斑不仅外形连里面也是一样的。

这种情况就叫做线性空间不变。 （注意，以上的讨论只是在理想透镜的情况下讨论的，当然我们引入了离焦，所以其实包含了低阶像差，但是更复杂的情况并没有仔细讨论，球差也是线性空间不变的，但如果成像面弯曲了，恐怕就不是这样了，但通常我们只考虑黄斑区那一点点的范围，这时候光斑几乎是相同的，称作“等晕区”，可以近似认为是线性空间不变的）。

一个相反的例子，哈哈镜，

哈哈镜是线性系统，一个光点成像不影响另一个光点的像。但如果你拿着一个点移动，透过哈哈镜看输出，随着点的位置不同，放大、扭曲、缩小的情况各不相同，所以哈哈镜是线性的，但不是线性空间不变的。