公理设计笔记(3)
前面讲解了目的,要尽量形成FRs(功能需求)与DPs(设计参数)的解耦合对应关系
尽量对角矩阵形成: $$ FRs=\begin{bmatrix} X & 0 & ... & 0 \\ 0 & X & ... & 0 \\ ... \\ 0 & 0 & ... & X \end{bmatrix} DPs $$
或者至少形成三角形矩阵: $$ FRs=\begin{bmatrix} X & 0 & ... & 0 \\ X & X & ... & 0 \\ ... \\ 0 & X & ... & X \end{bmatrix} DPs $$
实际过程中是分层级对FRs(功能需求)与DPs(设计参数)进行分解的。先从
$$ \begin{bmatrix} FR_1 \\ FR_2 \end{bmatrix} = \begin{bmatrix} X & 0 \\ X & X \end{bmatrix} \begin{bmatrix} DP_1 \\ DP_2 \end{bmatrix} $$开始,
然后再把$FR_1$(功能需求)拆解成$FR_{1.1}, FR_{1.2}$,变成类似这个意思:
$$ \begin{bmatrix} \begin{bmatrix} FR_{1.1} \\ FR_{1.2} \end{bmatrix} \\ FR_2 \end{bmatrix} = \begin{bmatrix} \begin{bmatrix} X & 0 \\ X & X \end{bmatrix}& 0 \\ X & X \end{bmatrix} \begin{bmatrix} \begin{bmatrix} DP_{1.1} \\ DP_{1.2} \end{bmatrix} \\ DP_2 \end{bmatrix} $$在拆分FRs(功能需求)的时候,要求是MECE min原则,也就是"不重复不漏项"并且总数尽量少。MECE := Mutually Exclusive Collectively Exhaustive,课程中使用的是CEME,可能商科里用MECE更多,反正一个意思。
比如3D打印机的FR(功能需求)之一是要求在$FR_1$打印头空间内移动,那么就可以拆分成:
- $FR_{1.1}$ 在X轴方向移动
- $FR_{1.2}$ 在Y轴方向移动
- $FR_{1.3}$ 在Z轴方向移动
这样的拆分方式显然是MECE的,当然也可以拆分成圆柱坐标系、球坐标系等等。不同的分解方式对应着不同的解决方案。
对于DPs(设计参数)的拆分,目的是尽量形成对角矩阵,或者至少是三角形矩阵,那么就应当尽量让右上角的区域保持为0。而且在拆分DPs(设计参数)的时候,约束条件是继承的,比如$DP_1$是在中国建厂,那么$DP_{1.1},DP_{1.2}$就不能把工厂建立到越南去。
在实际操作中,拆分是一点一点来进行的。说叫ZigZag。
先把$FR_1$(功能需求)拆解成$FR_{1.1}, FR_{1.2}$,拆分好$FR_1$(功能需求)以后,再去拆分$DP_1$(设计参数),拆好了DPs(设计参数)以后,再返回来拆下一个$FR$(功能需求)
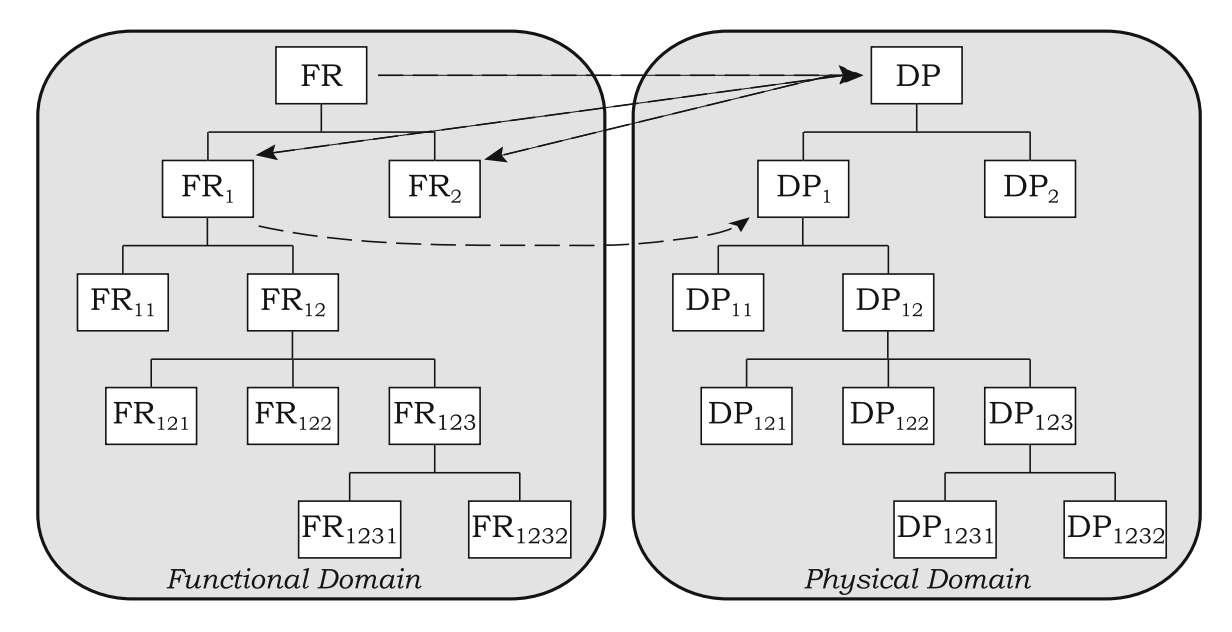
拆分过程可以用个电子表格来做,最好再弄成可折叠的,似乎有专用的软件可以画图,但不知道excel或者其他通用的简单工具有没有这样的功能。注意子节点上的相关性X,一定要表现在父节点上。比如检查时发现调整$DP_{2}$时$FR_{12}$也跟着变,那$DP_{2}$其实与$FR_1$就是耦合的,中间肯定在某个步骤出错了。
| FRs | $DP_1$ | $DP_{11}$ | $DP_{12}$ | $DP_{121}$ | $DP_{122}$ | $DP_{123}$ | $DP_{2}$ |
|---|---|---|---|---|---|---|---|
| $FR_1$ | X | X | 0 | 0 | 0 | 0 | X |
| $FR_{11}$ | $\space$ | X | 0 | 0 | 0 | 0 | 0 |
| $FR_{12}$ | $\space$ | X | X | 0 | 0 | 0 | X |
| $FR_{121}$ | |||||||
| $FR_{122}$ | |||||||
| $FR_{123}$ | |||||||
| $FR_{2}$ |
当有几个不同的拆分FRs(功能需求)的方法,得到了不同的DPs(设计参数)以后。如何判定那种方式更好呢?毫无疑问会陷入到办公室争吵中。
公理设计的第二条公理:
要令信息量最小
这里的信息量,是原教旨的信息量。记住这是MIT教授的书,WPI教授的课。
$$ I=-\sum_{i}^{\sigma(\mathrm{FR})} \log _{2} P_{i} $$其中$P_i$是$FR_i$实现的概率
在我理解,这只是实现概率最大化的恐怖公式表达而已。这一部分我还没有深究,毕竟我能想到一组DPs(设计参数)就已经不错了。
这个公理大约对硬件选型的时候更有意义,比如同一个目的,在资金约束条件下,要选精度高一点,冗余大一点的零件。